Když se volný kladný náboj q je urychlen v elektrickém poli, je dána kinetickou energii (viz Obrázek \(\PageIndex{1}\))., Proces je analogický objekt, je urychlena gravitačním poli, jako by se obvinění chystali dolů elektrický hill, kde jeho elektrická potenciální energie se přemění na kinetickou energii, i když samozřejmě zdroje síly jsou velmi odlišné. Pojďme prozkoumat práci vykonanou na náboj q elektrickým polem v tomto procesu, takže můžeme vyvinout definici energie elektrického potenciálu.

elektrostatická nebo Coulombova síla je konzervativní, což znamená, že práce na q je nezávislá na provedené cestě, jak ukážeme později., To je přesně analogické gravitační síle. Když je síla konzervativní, je možné definovat potenciální energii spojenou se silou. Obvykle je snazší pracovat s potenciální energií (protože závisí pouze na poloze), než přímo vypočítat práci.

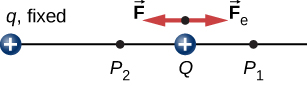
práce \(W_{12}\) provádí působící síly \(\vec{F}\), kdy se částice pohybuje od \(P_1\) k \(P_2\) lze vypočítat tím,

\

\

kde jsme definovali pozitivní směřující pryč od původu a r je vzdálenost od počátku. Směry jak posunutí, tak aplikované síly v systému na obrázku \(\PageIndex{2}\) jsou paralelní, a proto je práce na systému kladná.

používáme písmeno U K označení energie elektrického potenciálu, která má jednotky joulů (J)., Když konzervativní síla dělá negativní práci, systém získává potenciální energii. Když konzervativní síla dělá pozitivní práci, systém ztrácí potenciální energii, \(\Delta U = – W\). V systému na obrázku \(\PageIndex{3}\) Působí Coulombova síla v opačném směru než posunutí; proto je práce negativní. Zvýšili jsme však potenciální energii v systému dvou nábojů.

v tomto příkladu je práce W provedená pro urychlení pozitivního náboje z odpočinku pozitivní a je výsledkem ztráty U nebo negativního \(\Delta u\)., Hodnota pro U lze nalézt v libovolném bodě tím, že jeden bod jako odkaz a výpočet práce potřebné k přesunutí náboje do druhého bodu.

gravitační potenciální energie a energie elektrického potenciálu jsou zcela analogické. Potenciální energie představuje práci vykonanou konzervativní silou a poskytuje další pohled na transformaci energie a energie bez nutnosti přímého jednání se silou. Je mnohem běžnější například použít koncept elektrické potenciální energie, než se vypořádat s Coulombovou silou přímo v reálných aplikacích.,

\

všimněte si, že q je konstanta.

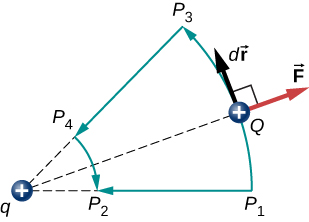
dalším důsledkem je, že můžeme definovat energii elektrického potenciálu. Připomeňme, že práce prováděná konzervativní silou je také vyjádřena jako rozdíl v potenciální energii odpovídající této síle., Proto je práce \(W_{ref}\) tak, aby napětí z referenčního bodu do bodu zájmu může být zapsáno jako

\

a tím, že Rovnici \ref{7.1}, rozdíl v potenciální energii (\(U_2 – U_1\)) zkušebního náboje Q mezi dvěma body je

\

Proto, můžeme zapsat obecný výraz pro potenciální energie dvou bodových nábojů (ve sférických souřadnicích):

\_{r_{ref}}^r = kqQ\left.,\]

Můžeme vzít druhý termín je libovolný konstantní referenční úrovně, které slouží jako nulová referenční číslo:

\

pohodlný výběr z odkazu, který se opírá o náš zdravý rozum je, že když se dva obvinění jsou nekonečně daleko od sebe, neexistuje žádná interakce mezi nimi. (Připomeňme diskusi o referenční potenciální energii v potenciální energii a zachování energie.,), Přičemž potenciální energie tohoto stavu nulová, odstraňuje výraz \(U_{ref}\) z rovnice (stejně jako když říkáme, že země je nulová potenciální energie v gravitačním potenciální problém energie), a potenciální energie Q, když je oddělen od q ve vzdálenosti r přijímá podobu

\

Vzhledem k Coulombův zákon, síly vzhledem k více poplatků na zkušební náboje \(Q\) překrýt; mohou být vypočteny individuálně a pak dodal. To znamená, že pracovní integrály a tím i výsledné potenciální energie vykazují stejné chování., Abychom to prokázali, uvažujeme o příkladu sestavení systému čtyř poplatků.

Všimněte si, že elektrické potenciální energie je pozitivní, pokud se dva obvinění jsou stejného typu, a to buď pozitivní, nebo negativní, a negativní, pokud dva obvinění jsou opačné typy. To dává smysl, pokud uvažujete o změně potenciální energie \(\Delta u\), když přiblížíte obě náboje nebo je posunete dále od sebe., V závislosti na relativních typech poplatků, možná budete muset pracovat na systému nebo systém bude pracovat na vás, to znamená, že vaše práce je buď pozitivní nebo negativní. Pokud musíte udělat pozitivní práci na systému (ve skutečnosti posunout náboje blíže), pak by se energie systému měla zvýšit. Pokud přiblížíte dvě kladné nebo dvě záporné náboje, musíte na systému udělat pozitivní práci, což zvyšuje jejich potenciální energii. Protože potenciální energie je úměrná 1 / r, potenciální energie stoupá, když r klesá mezi dvěma kladnými nebo dvěma zápornými náboji.,

Na druhou stranu, pokud si přinést pozitivní a negativní náboj blíže, co musíte udělat, negativní práci na systému (poplatky se stahují), což znamená, že budete mít energii pryč ze systému. To snižuje potenciální energii. Vzhledem k tomu, že potenciální energie je negativní v případě kladného a záporného náboje, zvýšení 1/r činí potenciální energii negativnější, což je stejné jako snížení potenciální energie.

výsledek z příkladu \(\PageIndex{2}\) může být rozšířen na systémy s libovolným počtem poplatků., V tomto případě, je nejvhodnější napsat vzorec,

\

faktor 1/2 účty pro přidání každá dvojice poplatky dvakrát.