Velmi neformálně, dva termíny v součtu dána Black-Scholes vzorec může být myšlenka jako ‚aktuální cena akcií vážený pravděpodobnost, že budete realizovat vaši opci k nákupu akcií „minus“ zvýhodněnou cenu výkonu možnost vážený pravděpodobnost, že budete cvičit možnost‘, nebo jednoduše to, co se chystáte dostat „minus“, co budete platit‘ (Khan, 2013).,

U Evropské opce (smluv o právo, ale ne povinnost, prodat některé podloží aktiva za předem stanovenou cenu v předem stanovené datum v budoucnosti) ekvivalent funkční forma je:

Příklad: Výpočet ceny Evropské call opce

aby bylo možné vypočítat to, co je cena Evropské call opce by měla být, víme, že potřebujeme pět hodnot požadovaných podle rovnice 6 výše. Jsou: 1. Aktuální cena akcií, 2. Cena hovoru (X), 3. Čas vypršení (T-t), 4. Bezriziková úroková sazba (r) a 5., Volatilita akcií, daná směrodatnou odchylkou historických návratů log (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

můžeme odhadnout akciové volatility tím, že sleduje své historické ceny, nebo, ještě jednodušší, na základě výpočtu jiná možnost ceny za stejné populace za různé splatnosti/expirace (T) a cvičení/realizační ceny (X), pokud víme, že byly stanoveny podle Black-Scholes model. Výsledná hodnota σ je číslo mezi 0 a 1, což představuje implikovanou volatilitu trhu pro akcie., Pro Tesla, v době psaní tohoto článku, hodnota v průměru přibližně 0.38 4-5 různých cen opcí kolem stejné platnosti/splatnost. Vstup do rovnice 6 výše, zjistíme, že možnost volání máme zájem by měly být ceny někde kolem $7.

Implikovaná volatilita

i když je zajímavé pochopit, jak volby emitentů dorazí za cenu jejich call a put opce, protože investoři je těžké „nesouhlasím“ s takovými cenami, per se, a tak těžké proměnit tyto znalosti do žalovatelné investiční teze.,

můžeme však získat spoustu kilometry z Black-Scholes vzorec, pokud budeme místo toho léčit ceny opce (C nebo P) jako známé množství/nezávislé proměnné (nalézt při pohledu na různé splatnosti/data vypršení platnosti T a různých cvičení cen X). To proto, že pokud ano, funkční rovnice Black-Scholes se stává nástrojem, který nám pomůže pochopit, jak trh odhaduje volatilitu akcie, známou také jako implikovaná volatilita opce. To jsou informace, se kterými se můžeme neshodnout, a obchodujeme proti.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called „continuous timeline instruments”), they are much more difficult to deal with that European options („point in time instruments”)., Především proto, že optimální politika cvičení ovlivní hodnotu možnosti, je třeba to vzít v úvahu při řešení parciální diferenciální rovnice Black-Scholes. Neexistují žádná známá řešení „uzavřené formy“ pro americké možnosti podle rovnice Black-Scholes. Existují však některé speciální případy:

• Pro Americké opce na podkladová aktiva, které neplatí dividendy (nebo další výplaty), Americká call opce, cena je stejná jako u Evropské call opce. To proto, že optimální politika cvičení v tomto případě je nevyužít tuto možnost.,
• u amerických opcí na podkladová aktiva, která vyplácejí jednu známou dividendu za její životnost, může být optimální tuto možnost uplatnit brzy., V takových případech možnost může být optimálně uplatnit těsně předtím, než jde ex-dividend, v závislosti na řešení dané v uzavřené formě tzv. Roll-Geske-Whaley metoda (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

Nejprve zkontrolujte, zda je optimální opci, brzy, tím, že zkoumá, zda následující nerovnost je splněna:

Pro S = cena akcie, X = realizační cena, D₁ = dividenda vyplacena, t = aktuální datum, t₁ = datum výplaty dividendy, T = datum vypršení platnosti možnost.

není-li nerovnost splněna, časné cvičení není optimální., Pokud C(・) je pravidelné Black-Scholes vzorec pro Evropské opce call na non-dividend-platit akcií (eq, x), je hodnota Americké call opce je pak dána verzi stejné rovnice, kde se cena akcie (S) je zlevněné:

v Případě, že nerovnost je splněna, začátkem cvičení je optimální a hodnota Americké call opce je dána tímto, příšerné, nepořádek rovnice (snažil jsem se zlomit to tím, že každý termín, aby byl čitelný):

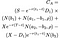
Kde, jak, než S = cena akcie, T = datum vypršení opce, X = realizační cena a r = bezriziková úroková míra, σ = volatilita cen (standardní odchylka protokolu o historické výnosy z akcií), a D₁ se výplaty dividend. Kromě toho, ρ je dána:

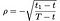
a₁, a₂ by:

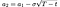
and b₁, b₂ by:

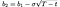
Omezení

To by měl jít bez říká, že Black-Scholes model je právě to, že teoretický model, který se snaží odhadnout, jak se trh chová, vzhledem k tomu předpoklady je uvedeno výše, a inherentní omezení naší vlastní číselný odhad bezrizikové úrokové míry (r) a budoucí volatilitu (σ). Zde je třeba zdůraznit, že ne všechny předpoklady (zejména původní model) jsou ve skutečnosti empiricky platné., Například významné omezení vyplývají z:

• podcenění extrémní pohyby na skladě, poddajný ocas riziko
• předpoklad, rychlé, nákladově méně obchodování, získávání likvidity, rizika
• předpoklad stacionární proces, přinášející riziko volatility
• předpoklad nepřetržitého času a obchodování, výtěžkem mezera riziko

Ty by měly být zaúčtovány v jakékoliv a všech investičních strategií, například zajištění, s out-of-the-money opce, obchodování na více trzích, zajištění s volatilita zajištění a Gama hedging, resp.,

Pozadí

Jak se krátce zmínil to byl Fischer Black a Myron Scholes, který v roce 1973 ukázala, že dynamicky revizi portfolia podle určitých pravidel odstraní očekávaný výnos podkladového cenného papíru (Black & Scholes, 1973). Jejich model postavený na dříve zavedených dílech Bacheliera, Samuelsona a dalších. Robert C. Merton byl první publikovat papír rozšiřuje na pochopení model a, který razil termín „Black-Scholes model oceňování opcí“., Scholes a Merton byl oceněn 1997 Nobelovu cenu Memorial Prize v ekonomických vědách za jejich objev způsobu rozvodu akciových opcí z rizika jejich podkladových cenných papírů. Když Fischer Black zemřel v roce 1995, neměl nárok na udělení ceny, ale byl uznán jako přispěvatel Nobelovy Akademie.