Jednoduché stroje – jak fungují kola a nápravy?
Eugene je kvalifikovaný ovládání/instrumentation engineer Bsc (Eng) a pracoval jako vývojář elektroniky & software pro SCADA systémy.

Hvězda
.,com,
Kol a Náprav — Jeden ze Šesti Klasických Jednoduchých Strojů
Kola jsou všude, v naší moderní technologické společnosti, ale mají také používá od starověku. Místo, kde s největší pravděpodobností uvidíte kolo, je na vozidle nebo přívěsu, ale kola se používají pro řadu dalších aplikací. Jsou široce používány ve strojích ve formě ozubených kol, řemenic, ložisek, válečků a závěsů. Kolo se spoléhá na páku, aby se snížilo tření.,
kolo a náprava jsou jedním ze šesti klasických jednoduchých strojů definovaných renesančními vědci, mezi něž patří také páka, kladka, klín, nakloněná rovina a šroub.
než si přečtete toto vysvětlení, které se stává trochu technickým, bylo by užitečné přečíst si další související článek, který vysvětluje základy mechaniky.,
síla, hmotnost, zrychlení a jak porozumět Newtonovým zákonům pohybu
historie kola
kola pravděpodobně nebyla vynalezena pouze jednou osobou a pravděpodobně se vyvinula v mnoha civilizacích nezávisle na tisíciletí. Můžeme si jen představit, jak se to stalo. Možná si nějaká jasná jiskra všimla, jak snadné bylo posunout něco přes zem se zaoblenými kamennými oblázky na něm, nebo pozorovat, jak snadno lze kmeny stromů válcovat, jakmile se kácet. První „kola“ byly pravděpodobně válečky vyrobené z kmenů stromů a umístěné pod těžkými břemeny., Problém s válečky je, že jsou dlouhé a těžké a musí být neustále znovu-umístěny podle zatížení, takže náprava musel být vynalezen, aby držet tenčí disk, účinně kola, na místě. Časná kola byla pravděpodobně vyrobena z kamene nebo plochých desek spojených do podoby disku.
Moment síly
abychom pochopili, jak fungují kola a páky, musíme pochopit koncept momentu síly. Moment síly kolem bodu je velikost síly vynásobená kolmou vzdáleností od bodu k linii síly.,
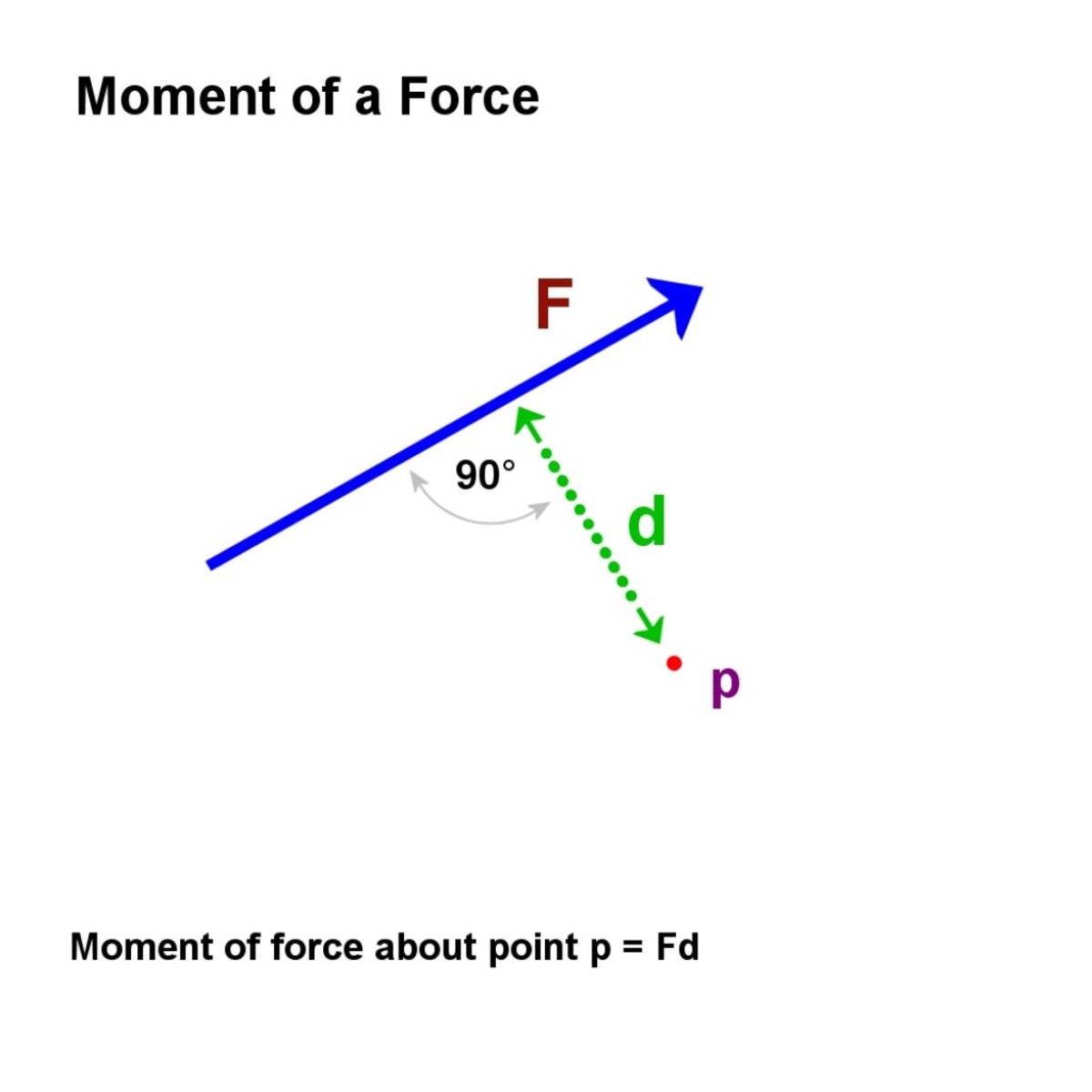
Moment síly.
Image © Eugbug
proč kola usnadňují tlačit věci?
to vše se scvrkává na snížení tření. Takže si představte, že máte těžkou váhu spočívající na zemi. Newtonův 3.zákon uvádí, že „pro každou akci existuje stejná a opačná reakce“. Takže když se pokusíte zatlačit zatížení, síla přenáší zátěž na povrch, na kterém spočívá., Tohle je akce. Odpovídající reakcí je síla tření působící dozadu a závisí jak na povaze povrchů, které jsou v kontaktu, tak na hmotnosti zátěže. Toto je známé jako statické tření nebo lepení a vztahuje se na suché povrchy v kontaktu. Zpočátku reakce odpovídá akci velikosti a zatížení se nepohybuje, ale nakonec, pokud zatlačíte dostatečně tvrdě, třecí síla dosáhne limitu a dále se nezvyšuje. Pokud zatlačíte tvrději, překročíte mezní třecí sílu a zatížení se začne posouvat., Síla tření se však nadále staví proti pohybu (to trochu snižuje, jakmile pohyb začíná), a v případě, že zatížení je velmi těžký a/nebo povrchy v kontaktu mají vysoký koeficient tření, to může být obtížné, aby se snímek.
kola eliminují tuto třecí sílu pomocí pákového efektu a nápravy. Stále potřebují tření, aby se mohli „zatlačit“ na zem, na které se valí, jinak dojde k prokluzu. Tato síla však není proti pohybu nebo ztěžuje otáčení kola.,
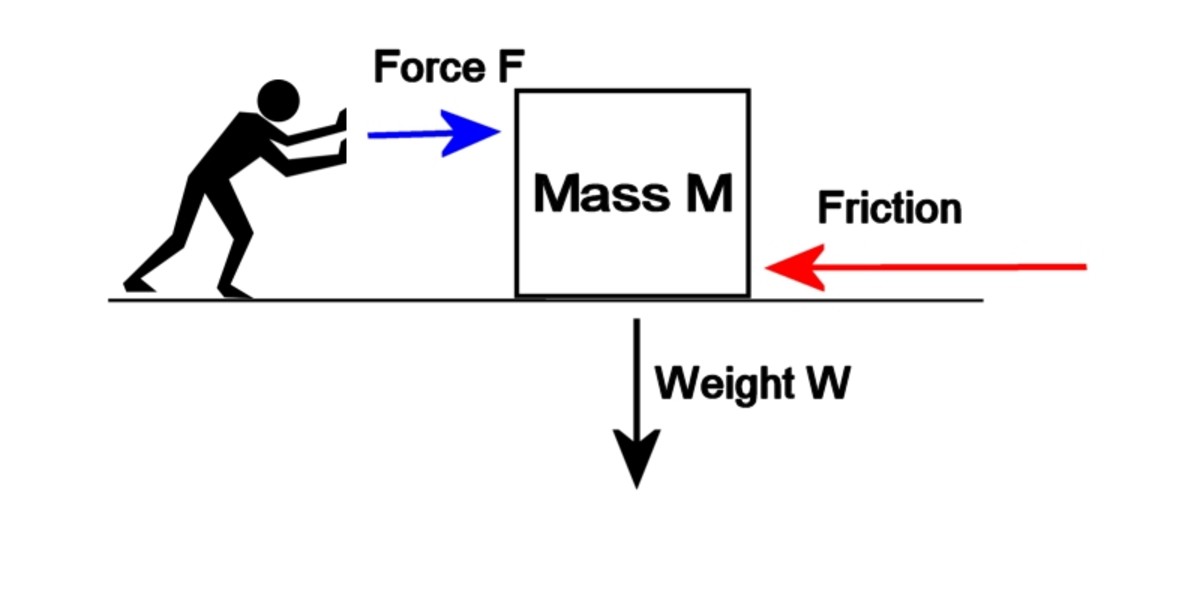
Friction can make sliding difficult
Image © Eugbug
Pushing a Cart With a Load – Wheels Make it Easier
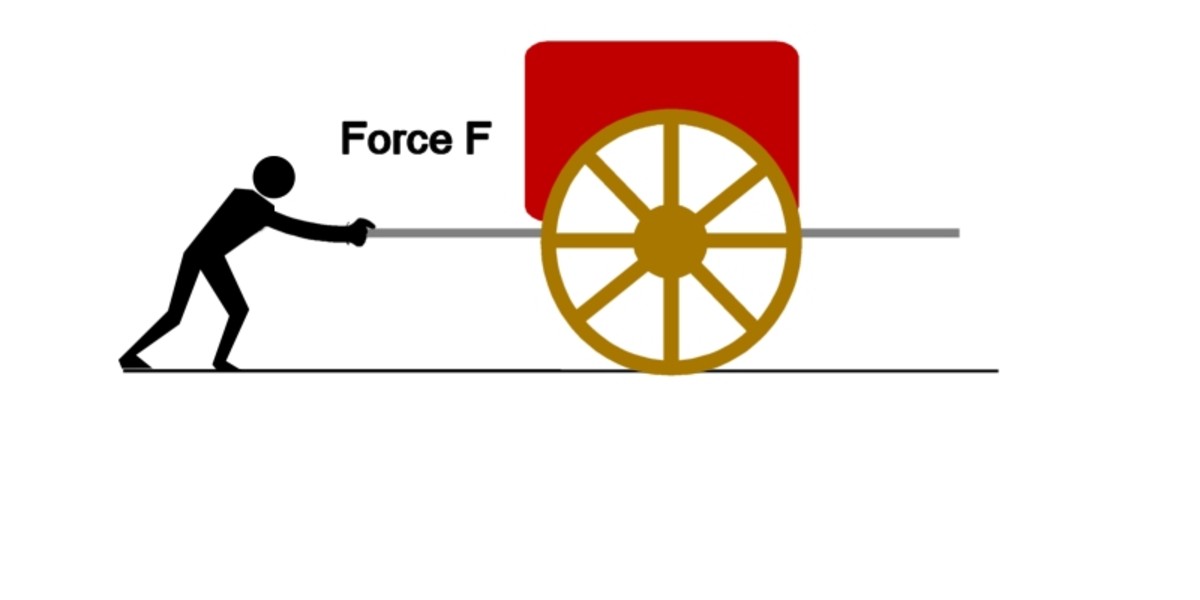
Pushing a cart with a load. Wheels make it easier
Image © Eugbug
How Do Wheels Work?,
Rozbor Kola vlivem Síly na Nápravy
Tato analýza se vztahuje na výše uvedený příklad, kde kolo je předmětem síly nebo intenzity F na nápravu.
Obr. 1
síla působí na nápravy, jehož poloměr je d.
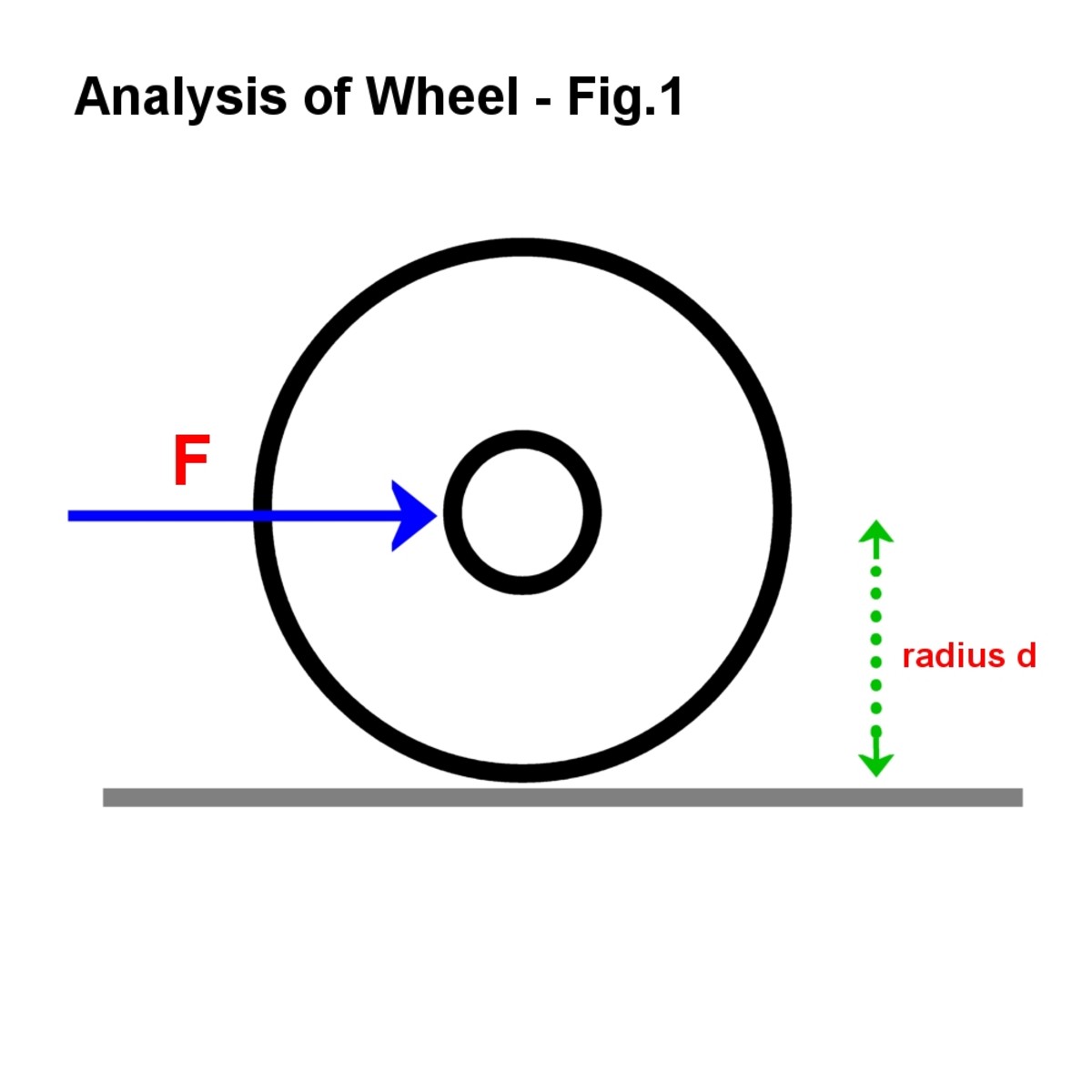
Obrázek © Eugbug
Obr. 2
jsou zavedeny dvě nové stejné, ale protilehlé síly, kde se kolo setkává s povrchem., Tato technika přidávání fiktivních sil, které se navzájem ruší, je užitečná pro řešení problémů.
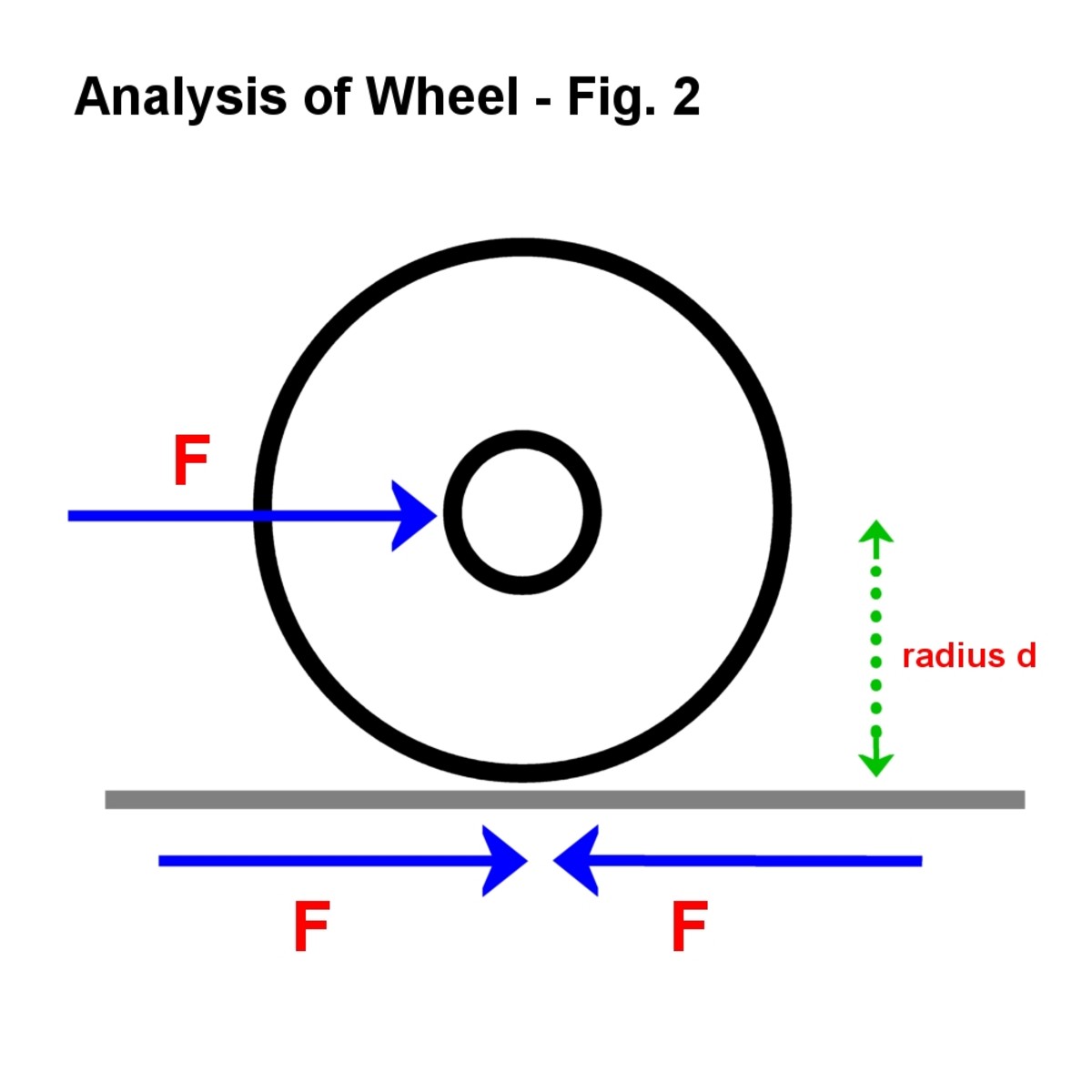
Přidat 2 fiktivní síly F
Obrázek © Eugbug
Obr. 3
Když dvě síly působí v opačných směrech, výsledek je známý jako pár a jeho velikost se nazývá točivý moment. V diagramu mají přidané síly za následek Pár plus aktivní sílu, kde se kolo setkává s povrchem., Velikost tohoto páru je síla vynásobená poloměrem kola.
takže točivý moment Tw = Fd.
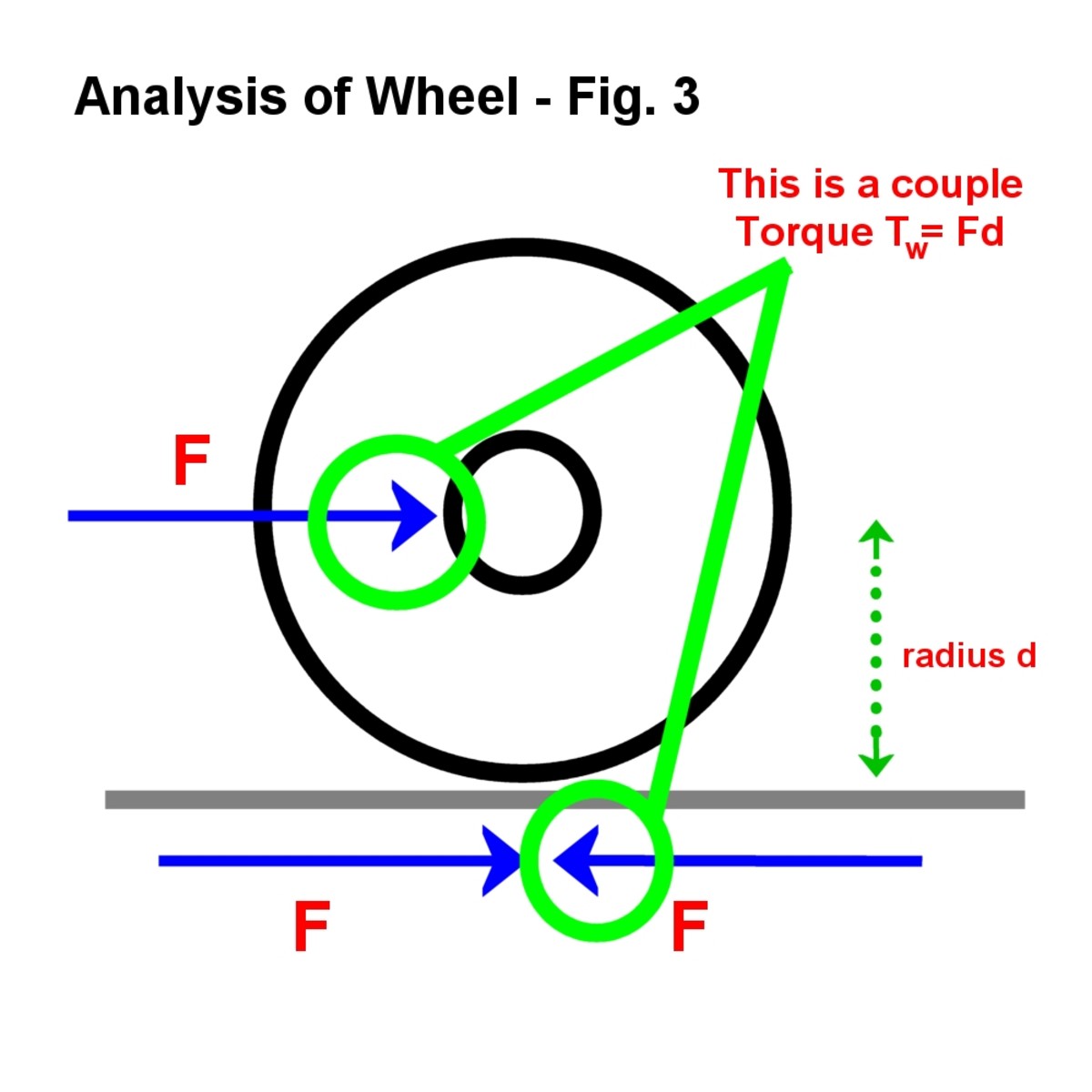
2 síly, tvoří pár,
Obrázek © Eugbug
Obr. 4
hodně se děje tady! Modré šipky označují aktivní síly, fialové reakce. Točivý moment Tw, který nahradil dvě modré šipky, Působí ve směru hodinových ručiček., Opět přichází do hry Newtonův třetí zákon a na nápravě je omezující reaktivní točivý moment Tr. To je způsobeno třením způsobeným hmotností na nápravě. Rez může zvýšit mezní hodnotu, mazání ji snižuje.
dalším příkladem je, když se pokusíte vrátit matici, která je zrezivělá na šroub. Aplikujete točivý moment klíčem, ale rez váže matici a působí proti vám. Pokud použijete dostatek točivého momentu, překonáte reaktivní točivý moment, který má mezní hodnotu. Pokud je matice důkladně zachycena a aplikujete příliš mnoho síly, šroub se vyždímá.,
Ve skutečnosti, věci jsou složitější, a tam je další reakce vzhledem k momentu setrvačnosti kola, ale nebudeme to komplikovat a předpokládat, že kola jsou ve stavu beztíže!
- hmotnost působící na kola vzhledem k hmotnosti vozíku je W
- reakce na povrchu země je Rn = W
- k Dispozici je také reakce na volant/povrch rozhraní vzhledem k síle F působící dopředu. To není proti pohybu, ale pokud je to nedostatečné, kolo se neotáčí a bude klouzat. To se rovná F a má mezní hodnotu Ff = uRn.,
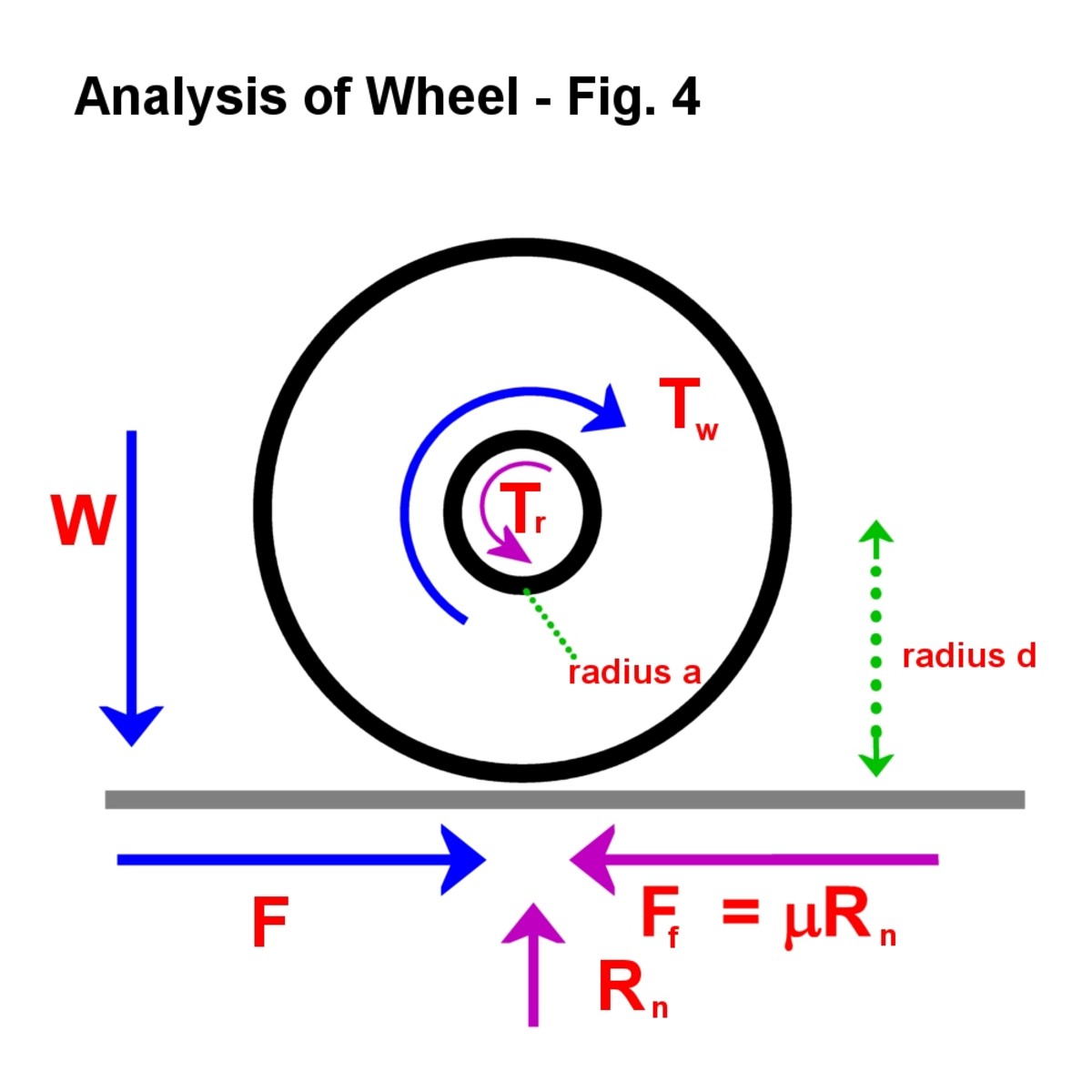
Reactions at the ground and axle
Image © Eugbug

Undoing a nut. The limiting value of friction must be overcome to release the nut
Image © Eugbug
Fig., 5
obě síly, které produkují točivý moment Tw, jsou opět zobrazeny. Nyní můžete vidět, že se podobá pákovému systému, jak je vysvětleno výše. F působí na vzdálenost d a reakce na nápravě je Fr.
síla F je zvětšena na nápravě a je zobrazena zelenou šipkou. Jeho velikost je:
Fe = F (d/a)
protože poměr průměru kola k průměru nápravy je velký , tj. Kolo účinně funguje jako páka, zvětšuje sílu na nápravě a překonává mezní hodnotu třecí síly Fr., Všimněte si také pro daný průměr nápravy a, pokud je průměr kola větší, Fe se zvětší. Takže je snazší tlačit něco s velkými koly než malými koly, protože na nápravě je větší síla k překonání tření.
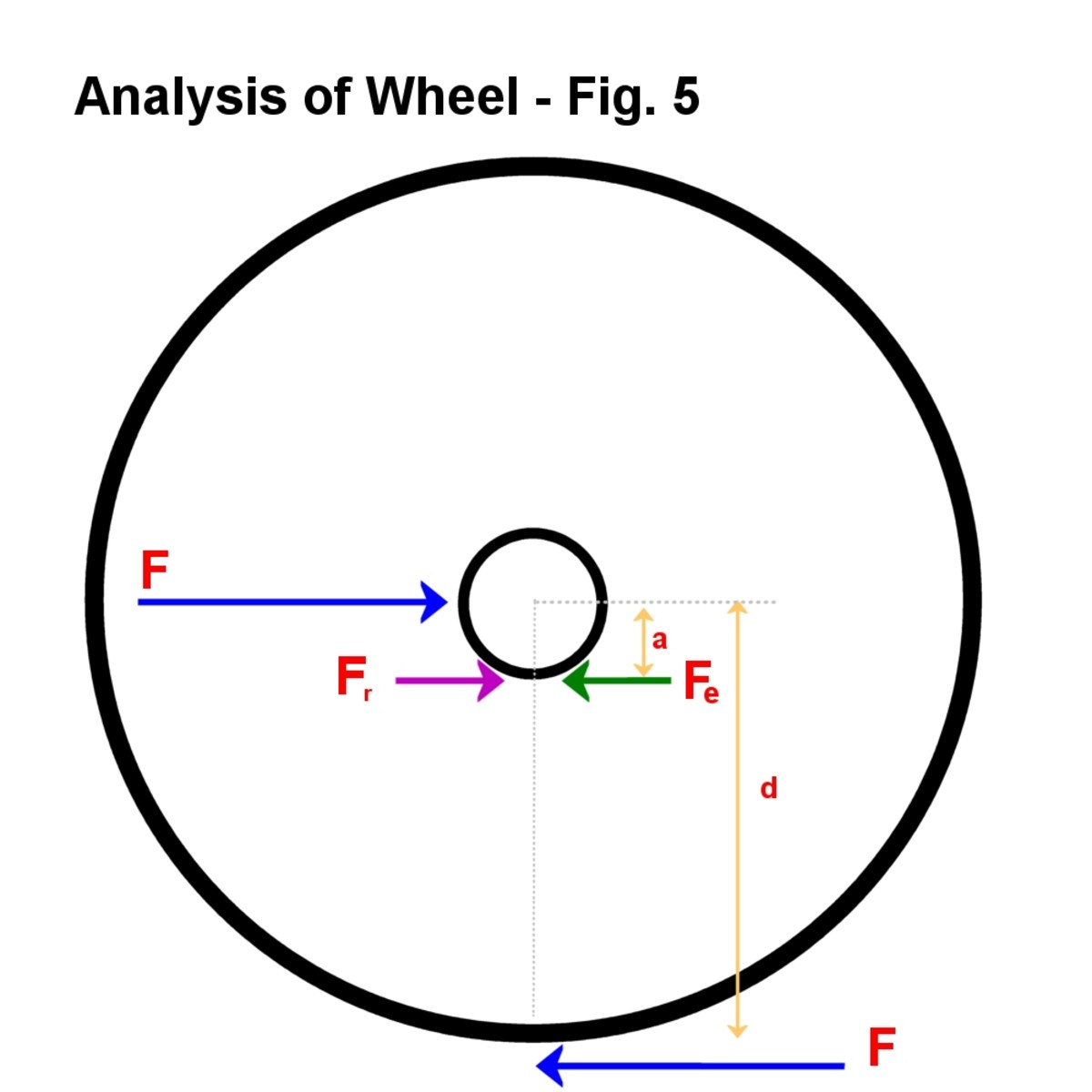
aktivní a reaktivní síly na nápravy
Obrázek © Eugbug
, Která je Lepší, Velká Kola, nebo na Malá Kola?,
, Protože
Točivý moment = Síla na Nápravu x Poloměr Kola
pro danou sílu na nápravu, točivý moment působící na nápravy je větší pro větší kola. Takže tření na nápravě je značně překonáno, a proto je snazší tlačit něco s většími koly. Také pokud povrch, na kterém se kolo valí, není příliš plochý, kola s větším průměrem mají tendenci překlenovat nedokonalosti, což také snižuje požadované úsilí.,
Když se kola poháněné nápravy, protože
Točivý moment = Síla na Nápravu x Poloměr Kola
proto
Síly na Nápravy = Točivý moment / Poloměr Kola
pro konstantní hnací točivý moment, menší průměr kola produkovat větší tažné síly na nápravě, než větší kola. To je síla, která tlačí vozidlo.
Otázky & Odpovědi
Otázka: Jak se kolo snížit úsilí?
odpověď: odstraňuje kinetické tření, které je proti pohybu vpřed, když je objekt sklouzán a nahrazuje jej třením při bití nápravy/kola., Zvýšení průměru kola snižuje toto tření úměrně.















