Articles

Komutativní, asociativní a distribuční zákony

by admin

Wow! To je ale sousto slov! Ale myšlenky jsou jednoduché.

komutativní zákony

„komutativní zákony“ říkají, že můžeme zaměnit čísla a stále získat stejnou odpověď …

… když přidáme:

a + b = b + a

příklad:

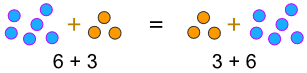
… nebo když vynásobíme

a × b = b × a

Příklad:

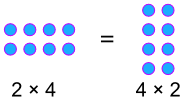
Komutativní Procenta!,

Protože a × b = b × a je také pravda, že a% b = b% a

Příklad: 8% z 50 = 50% 8, což je 4

Proč „komutativní“ … ?

protože čísla mohou cestovat tam a zpět jako dojíždějící.

Asociativní Zákony

„Asociativní Zákony“, říkají, že nezáleží na tom, jak jsme skupinu čísel (tj. který můžeme vypočítat jako první) …

…, když přidáme:

(a + b) + c = a + (b + c)

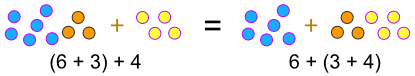
…,r>

: (2 + 4) + 5 = 6 + 5 = 11 Má stejnou odpověď jako toto: 2 + (4 + 5) = 2 + 9 = 11

: (3 × 4) × 5 = 12 × 5 = 60
Má stejnou odpověď jako toto: 3 × (4 × 5) = 3 × 20 = 60

Použití:

Někdy je jednodušší přidat nebo násobit v jiném pořadí:

Co je 19 + 36 + 4?,

19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59

Nebo uspořádat malý:

Co je 2 × 16 × 5?

2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160

Distributivní Zákon

„Distributivní Zákon“ je ten NEJLEPŠÍ ze všech, ale potřebuje pozornost.,

Tohle je to, co nám umožňuje udělat:

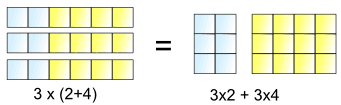
3 hodně (2+4) je stejné jako 3, spousta 2 plus 3 hodně 4

Takže 3× mohou být „rozloženy“ přes 2+4, do 3×2 a 3×4,

A můžeme to napsat takhle:

a × (b + c) = a × b + a × c,

Zkuste výpočty se sami sebe:

  • 3 × (2 + 4) = 3 × 6 = 18
  • 3×2 + 3×4 = 6 + 12 = 18

buď jak Buď dostane stejnou odpověď.,

V češtině můžeme říct:

dostaneme stejnou odpověď, když jsme se:

  • vynásobíme číslo u skupiny čísla se sčítají, nebo
  • násobit každý zvlášť a pak je přidat

Použití:

Někdy je jednodušší rozbít obtížné násobení:

Příklad: kolik je 6 × 204 ?

6 × 204 = 6×200 + 6×4
= 1,200 + 24
= 1,224

Nebo kombinovat:

Příklad: Jaký je 16 × 6 + 16 × 4?,

16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160

můžeme to použít v odčítání:

Příklad: 26×3 – 24×3

26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6

mohli Bychom to použít pro dlouhý seznam doplňků:

Příklad: 6×7 + 2×7 + 3×7 + 5×7 + 4×7

6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140

. . . ale Nechoďte příliš daleko!,

Komutativní Zákon nefunguje pro odčítání a dělení:

Příklad:

  • 12 / 3 = 4, ale
  • 3 / 12 = ¼

Asociativní Zákon nefunguje pro odčítání a dělení: