Návrat na Lekce Index | Lekce v Pořadí | Print-friendly stránku

Racionální Kořeny Test: Úvod (stránka 1 z 2)

nulového polynomu je vstupní hodnota (obvykle x-hodnota), která vrátí hodnotu nula pro celý polynom, když jej zapojíte do polynomu. Není složité) číslo, je to také X-intercept grafu polynomiální funkce., Často (zejména v počtu) budete chtít znát umístění nul dané polynomiální funkce. Můžete zapojit čísla do polynomu, chtě nechtě, a doufat v to nejlepší. Ale jak jste se dozvěděli, když jste studovali kvadratický vzorec, nuly jsou často velmi chaotická čísla; náhodné hádání pravděpodobně není nejlepší plán útoku. Tak jak se člověk snaží najít nuly?

test Rational Roots (nebo Rational Zeroes) je šikovný způsob, jak získat seznam užitečných prvních odhadů, když se snažíte najít nuly (kořeny) polynomu., Daný polynom s celočíselnými (to znamená, že pozitivní a negativní „celé číslo“) koeficienty, možné (nebo potenciální) nuly se nacházejí výpis faktory konstantní (poslední) termín za faktory vedoucí koeficient, a tak vytvořit seznam frakcí. Tento seznam vám dává seznam potenciálních racionálních (frakčních) kořenů, které chcete otestovat-odtud název testu.

dovolte mi zdůraznit: test racionálních kořenů vám nedává nuly. Neříká, jaké nuly určitě budou., Test vám dává pouze seznam relativně snadných a“ pěkných “ čísel, která můžete vyzkoušet v polynomu. Většina z těchto možných nul se ukáže, že ve skutečnosti nejsou nuly!

můžete vidět smysl metodiky testu při pohledu na jednoduchý polynom. Vzhledem k kvadratickému 12×2 – 7x – 10 můžete použít kvadratický vzorec k nalezení nul, ale můžete také faktor získat 12×2 – 7x – 10 = (3x + 2)(4x-5). Nastavením dvou faktorů rovných nule získáte dva kořeny na x = – 2/3 a x = 5/4., Všimněte si, že jmenovatele „3“ a „4“ jsou faktory vedoucí coefficiant „12“, a čitatele „2“ a „5“ jsou faktory, které jsou konstantní termín „10“. To znamená, že nuly jsou frakce tvořené faktory konstantního termínu (10) nad faktory předního koeficientu (12). Všimněte si také, nicméně, že zlomky, jako jsou 5/6 a – 10/3 mohou být také vytvořeny tímto způsobem (a tedy být poskytována Testu), ale tyto další frakce nejsou ve skutečnosti nuly kvadratické.,

Tento vztah je vždy pravda: je-Li polynom nemá racionální kořeny, pak ty kořeny budou zlomky formě (plus nebo mínus) (faktor konstanta) / (koeficient, vedoucí koeficient). Nicméně, ne Všechny frakce této formy jsou nutně nuly polynomu. Ve skutečnosti se může stát, že žádná z takto vytvořených frakcí není ve skutečnosti nulou polynomu.

Všimněte si, že stále říkám „potenciální“ kořeny,“ možné „nuly“, pokud existují takové kořeny…“., Je to proto, že seznam frakcí generovaných testem Rational Roots je jen seznam potenciálních řešení. Nemusí být pravda, že některá z frakcí je ve skutečnosti řešením. Nemusí existovat žádné zlomkové kořeny! Například, vzhledem k tomu, x2 – 2, Racionální Kořeny Testy dává následující možné racionální nuly:

Ale vy už víte, že:

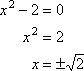
…takže nul vlastně nejsou racionální.,

vždy pamatujte: test Rational Roots poskytuje pouze seznam dobrých prvních odhadů; nedává vám „odpovědi“!

• Najděte všechny možné racionální x-zachycení x4 + 2×3 – 7×2-8x + 12.

Top | 1 | 2 | Return to Index Next >>