Wenn eine freie positive Ladung q durch ein elektrisches Feld beschleunigt wird, ist es gegebene kinetische Energie (Abbildung \(\pageIndex{1}\))., Der Prozess ist analog zu einem Objekt, das durch ein Gravitationsfeld beschleunigt wird, als würde die Ladung einen elektrischen Hügel hinuntergehen, wo ihre elektrische Potentialenergie in kinetische Energie umgewandelt wird, obwohl natürlich die Quellen der Kräfte sehr unterschiedlich sind. Lassen Sie uns die Arbeit an einer Ladung untersuchen, die durch das elektrische Feld in diesem Prozess erzeugt wird, damit wir eine Definition der elektrischen potentiellen Energie entwickeln können.

Die elektrostatische oder Coulomb-Kraft ist konservativ, was bedeutet, dass die Arbeit an q unabhängig vom eingeschlagenen Weg ist, wie wir später zeigen werden., Dies ist genau analog zur Gravitationskraft. Wenn eine Kraft konservativ ist, ist es möglich, eine potentielle Energie zu definieren, die mit der Kraft verbunden ist. Es ist normalerweise einfacher, mit der potentiellen Energie zu arbeiten (weil sie nur von der Position abhängt), als die Arbeit direkt zu berechnen.

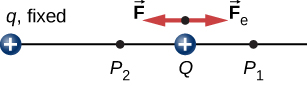
Die Arbeit \(W_{12}\), die mit der angewandten Kraft \(\vec{F}\) ausgeführt wird, wenn sich das Teilchen von \(P_1\) nach \(P_2\) bewegt, kann mit

\

\

berechnet werden, wobei wir positiv definiert haben, dass es vom Ursprung wegweist, und r der Abstand vom Ursprung ist. Die Richtungen sowohl der Verschiebung als auch der angewandten Kraft im System in Abbildung \(\pageIndex{2}\) sind parallel, und somit ist die Arbeit am System positiv.

Wir verwenden den Buchstaben U, um elektrische Potentialenergie zu bezeichnen, die Einheiten von Joule (J) hat., Wenn eine konservative Kraft nicht funktioniert, gewinnt das System potentielle Energie. Wenn eine konservative Kraft nicht funktioniert, verliert das System potentielle Energie, \(\Delta U = – W\). In dem System in Abbildung \(\pageIndex{3}\) wirkt die Coulomb-Kraft in die entgegengesetzte Richtung zur Verschiebung; Daher ist die Arbeit negativ. Wir haben jedoch die potentielle Energie im Zwei-Ladesystem erhöht.

In diesem Beispiel ist die Arbeit W zur Beschleunigung einer positiven Ladung aus dem Ruhezustand positiv und resultiert aus einem Verlust in U oder einem negativen \(\Delta U\)., Ein Wert für U kann an jedem Punkt gefunden werden, indem man einen Punkt als Referenz nimmt und die Arbeit berechnet, die benötigt wird, um eine Ladung auf den anderen Punkt zu verschieben.

Gravitationspotentialenergie und elektrische Potentialenergie sind ziemlich analog. Potenzielle Energie macht die Arbeit einer konservativen Kraft aus und gibt zusätzliche Einblicke in Energie und Energiewende, ohne direkt mit der Kraft umgehen zu müssen. Es ist viel häufiger, zum Beispiel das Konzept der elektrischen Potentialenergie zu verwenden, als direkt mit der Coulomb-Kraft in realen Anwendungen umzugehen.,

\

Beachten Sie, dass Q eine Konstante ist.

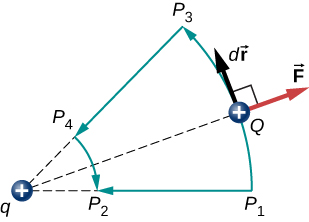
Eine weitere Implikation ist, dass wir eine elektrische Potentialenergie definieren können. Denken Sie daran, dass die Arbeit einer konservativen Kraft auch als Differenz in der potentiellen Energie ausgedrückt wird, die dieser Kraft entspricht., Daher kann die Arbeit \(W_{ref}\), um eine Ladung von einem Referenzpunkt zu einem Punkt von Interesse zu bringen, als

\

geschrieben werden, und durch Gleichung \ref{ref} ist die Differenz in der potentiellen Energie (\(U_2 – U_1\)) der Testladung Q zwischen den beiden Punkten

\

Daher können wir einen allgemeinen Ausdruck für die potentielle Energie von zwei Punktladungen (in sphärischen Koordinaten) schreiben:

\_{r_{ref}}^r = kqQ\links.,\]

Wir können den zweiten Term als eine beliebige konstante Referenzebene betrachten, die als Nullreferenz dient:

\

Eine bequeme Referenzwahl, die auf unserem gesunden Menschenverstand beruht, ist, dass, wenn die beiden Ladungen unendlich weit voneinander entfernt sind, keine Wechselwirkung zwischen ihnen besteht. (Erinnern Sie sich an die Diskussion über Bezugspotential Energie in Potentielle Energie und Energieeinsparung.,) Wenn man die potentielle Energie dieses Zustands auf Null setzt, wird der Term \(U_{ref}\) aus der Gleichung entfernt(genau wie wenn wir sagen, dass der Boden in einem Gravitationspotentialenergieproblem Nullenergie ist), und die potentielle Energie von Q, wenn sie durch einen Abstand von q getrennt wird, nimmt r die Form an

\

Aufgrund des Coulomb-Gesetzes überlagern sich die Kräfte aufgrund mehrerer Ladungen auf einer Testladung \(Q\); Sie können einzeln berechnet und dann addiert werden. Dies impliziert, dass die Arbeitsintegrale und damit die resultierenden potentiellen Energien das gleiche Verhalten aufweisen., Um dies zu demonstrieren, betrachten wir ein Beispiel für die Montage eines Systems von vier Ladungen.

Beachten Sie, dass die elektrische Potentialenergie positiv ist, wenn die beiden Ladungen vom gleichen Typ sind, entweder positiv oder negativ, und negativ, wenn die beiden Ladungen von entgegengesetzten Typen sind. Dies ist sinnvoll, wenn Sie an die Änderung der potenziellen Energie \(\Delta U\) denken, wenn Sie die beiden Ladungen näher bringen oder weiter auseinander bewegen., Abhängig von den relativen Arten von Gebühren müssen Sie möglicherweise am System arbeiten, oder das System würde an Ihnen arbeiten, dh Ihre Arbeit ist entweder positiv oder negativ. Wenn Sie positive Arbeiten am System ausführen müssen (die Ladungen tatsächlich näher bringen), sollte die Energie des Systems zunehmen. Wenn Sie zwei positive Ladungen oder zwei negative Ladungen näher bringen, müssen Sie positive Arbeiten am System ausführen, was ihre potentielle Energie erhöht. Da die Potentialenergie proportional zu 1/r ist, steigt die Potentialenergie, wenn r zwischen zwei positiven oder zwei negativen Ladungen sinkt.,

Wenn Sie andererseits eine positive und eine negative Ladung näher bringen, müssen Sie negative Arbeiten am System ausführen (die Ladungen ziehen Sie), was bedeutet, dass Sie dem System Energie entziehen. Dies reduziert die potentielle Energie. Da die potentielle Energie im Falle eines positiven und eines negativen Ladungspaares negativ ist, macht die Zunahme von 1/r die potentielle Energie negativer, was der Verringerung der potentiellen Energie entspricht.

Das Ergebnis von Example \(\pageIndex{2}\) kann auf Systeme mit beliebig vielen Ladungen erweitert werden., In diesem Fall ist es am bequemsten, die Formel als

\

zu schreiben, wobei der Faktor 1/2 für das zweifache Hinzufügen jedes Gebührenpaares verantwortlich ist.