Sehr informell, die beiden Begriffe in der Summe durch die Black-Scholes-Formel kann man sich als ‚der aktuelle Preis der Aktie gewichtet mit der Wahrscheinlichkeit, dass Sie üben Ihre option zum Kauf der Aktien‘ minus ‚der ermäßigte Preis der Ausübung der option, gewichtet mit der Wahrscheinlichkeit, dass Sie die option ausüben‘, oder einfach „das, was Sie sind gehen zu erhalten‘ minus‘, was Sie sind gehen zu zahlen “ (Khan, 2013).,

Für eine europäische Put-Option (Verträge über das Recht, aber keine Verpflichtung, einen unterlegenen Vermögenswert zu einem vorher festgelegten Preis zu einem vorher festgelegten Zeitpunkt in der Zukunft zu verkaufen) lautet die äquivalente Funktionsform:

Beispiel: Berechnung des Preises einer europäischen Call-Option

Um den Preis einer europäischen Call-Option zu berechnen, wissen wir, dass wir fünf Werte benötigen, die in Gleichung 6 oben erforderlich sind. Sie sind: 1. Der aktuelle Kurs der Aktie( En), 2. Der Ausübungspreis der call-option (X), 3. Die Zeit bis zum Ablauf (T-t), 4. Der risikofreie Zinssatz (r) und 5., Die Volatilität der Aktie, gegeben durch die Standardabweichung der historischen Log-Renditen (σ).

Wir können die Volatilität jeder Aktie durch Beobachtung ihrer historischen Preise oder, noch einfacher, durch Berechnung anderer Optionspreise für dieselbe Aktie zu unterschiedlichen Fälligkeits-/Ablaufdaten (T) und Ausübungs – /Ausübungspreisen (X) schätzen, wenn wir wissen, dass sie nach einem Black-Scholes-Modell festgelegt wurden. Der resultierende Wert σ ist eine Zahl zwischen 0 und 1, die die implizite Volatilität des Marktes für die Aktie darstellt., Zum Beispiel zum Zeitpunkt des Schreibens dieses Artikels, der Wert bei etwa 0,38 für 4-5 verschiedene Optionspreise um den gleichen Ablauf/Fälligkeit gemittelt. Eingabe in Gleichung 6 oben stellen wir fest, dass die Anrufoption, an der wir interessiert sind, Preise irgendwo um $7 sein sollte.

Implizite Volatilität

Obwohl es interessant ist zu verstehen, wie Optionsemittenten zum Preis ihrer Call-und Put-Optionen kommen, ist es für Anleger schwierig, solchen Preisen per se zu „widersprechen“ und dieses Wissen in umsetzbare Anlagenthesen umzuwandeln.,

Aus der Black-Scholes-Formel können wir jedoch viel Meilenzahl herausholen, wenn wir stattdessen den Preis einer Option (C oder P) als bekannte Menge/unabhängige Variable behandeln (gefunden durch Betrachten verschiedener Fälligkeits – /Ablaufdaten T und unterschiedlicher Ausübungspreise X). Dies liegt daran, dass die Black-Scholes-Funktionsgleichung in diesem Fall zu einem Werkzeug wird, um zu verstehen, wie der Markt die Volatilität einer Aktie schätzt, die auch als implizite Volatilität der Option bezeichnet wird. Dies sind Informationen, denen wir widersprechen und gegen die wir handeln können.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called „continuous timeline instruments”), they are much more difficult to deal with that European options („point in time instruments”)., Da sich die optimale Übungspolitik in erster Linie auf den Wert der Option auswirkt, muss dies bei der Lösung der partiellen Differentialgleichung von Black-Scholes berücksichtigt werden. Es sind keine „geschlossenen“ Lösungen für amerikanische Optionen nach der Black-Scholes-Gleichung bekannt. Es gibt jedoch einige Sonderfälle:

• Für amerikanische Call-Optionen auf Basiswerte, die keine Dividende (oder andere Auszahlungen) zahlen, ist der amerikanische Call-Optionspreis derselbe wie für europäische Call-Optionen. Dies liegt daran, dass die optimale Übungspolitik in diesem Fall darin besteht, die Option nicht auszuüben.,
• Für American Call-Optionen auf Basiswerte, die eine bekannte Dividende in ihrer Lebensdauer zahlen, kann es optimal sein, die Option frühzeitig auszuüben., In solchen Fällen kann die Option nach einer Lösung, die in geschlossener Form durch die sogenannte Roll-Geske-Whaley-Methode (Roll, 1977; Geske, 1979; 1981; Whaley, 1981) gegeben wurde, kurz vor dem Dividendenausschütten der Aktie optimal ausgeübt werden:

Überprüfen Sie zunächst, ob es optimal ist, die Option frühzeitig auszuüben, indem Sie untersuchen, ob die folgende Ungleichung erfüllt ist:

Für S = Aktienkurs, X = Ausübungspreis, d₁ = gezahlte Dividende, t = aktuelles Datum, t₁ = Datum der Dividendenzahlung, T = Ablaufdatum der Option.

Wenn die Ungleichung nicht erfüllt ist, frühe Übung es nicht optimal., Wenn C(・) ist die regelmäßige Black-Scholes-Formel für Europäische call-Optionen auf non-dividend-paying stock (eq, x), der Wert der amerikanischen call-option ist dann gegeben durch eine version der gleichen Gleichung, wo die Aktienkurse (S) ermäßigt:

Wenn die Ungleichung erfüllt ist, ist die Übung optimal und der Wert der American call Option wird durch das folgende, schreckliche Durcheinander einer Gleichung angegeben (ich habe versucht, sie durch jeden Begriff aufzubrechen, um sie lesbarer zu machen):

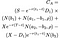
Wobei nach wie vor S = Aktienkurs, T = Ablaufdatum der Option, X = Ausübungspreis und r = risikofreier Zinssatz, σ = Volatilität (Standardabweichung des Protokolls der historischen Renditen der Aktie) und d₁ die Dividendenauszahlung ist. In addition, ρ) ist gegeben durch:

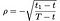
a₁, a₂ by:

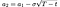
and b₁, b₂ by:

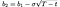
Limitations

Es sollte selbstverständlich sein, dass Black-Scholes-Modell genau das ist, ein theoretisches Modell, das versucht zu schätzen, wie sich ein Markt verhält, angesichts der oben genannten Annahmen und der inhärenten Einschränkungen unserer eigenen numerischen Schätzungen risikofreier Zinssätze (r) und zukünftiger Volatilität (σ). Es sollte hier hervorgehoben werden, dass nicht alle Annahmen (insbesondere das ursprüngliche Modell) tatsächlich empirisch gültig sind., Zum Beispiel ergeben sich erhebliche Einschränkungen aus:

• Die Unterschätzung extremer Bewegungen in der Aktie, das Tail-Risiko
• Die Annahme eines sofortigen, kostenlosen Handels, das Liquiditätsrisiko
• Die Annahme eines stationären Prozesses, das Volatilitätsrisiko
• Die Annahme eines kontinuierlichen Zeit-und Handels, das Gap-Risiko

Diese sollten in allen Anlagestrategien berücksichtigt werden, zum Beispiel durch Absicherung mit Out-of-the-Money-Optionen, Handel an mehreren Börsen, Absicherung mit Volatilitätsabsicherung bzw. Gamma-Absicherung.,

Hintergrund

Wie kurz erwähnt, zeigten Fischer Black und Myron Scholes 1973, dass eine dynamische Überarbeitung eines Portfolios nach bestimmten Regeln die erwartete Rendite des zugrunde liegenden Wertpapiers beseitigt (Black & Scholes, 1973). Ihr Modell basiert auf zuvor etablierten Werken von Bachelier, Samuelson und anderen. Robert C. Merton war der erste, der ein Papier veröffentlichte, das das Verständnis des Modells erweiterte und den Begriff „Black-Scholes options Pricing model“prägte., Scholes und Merton wurden 1997 mit dem Nobelpreis für Wirtschaftswissenschaften für ihre Entdeckung der Methode zur Trennung von Aktienoptionen vom Risiko ihrer zugrunde liegenden Wertpapiere ausgezeichnet. Als Fischer Black 1995 verstarb, wäre er nicht berechtigt, die Auszeichnung zu erhalten, wurde aber von der Nobelakademie als Mitwirkender anerkannt.