Zurück zu den Lektionen-Index | die Lektionen in Ordnung | Print-friendly page

Die Rational Roots Test: Einleitung (Seite 1 von 2)

Die null ein Polynom ist eine input-Wert (in der Regel ein x-Wert) gibt einen Wert von null für das ganze Polynom, wenn Sie stecken Sie es in das Polynom. Wenn eine Null eine reelle (dh nicht komplexe) Zahl ist, ist sie auch ein x-Intercept des Graphen der Polynomfunktion., Sie werden häufig (besonders in der Kalkulation) die Position der Nullen einer gegebenen Polynomfunktion kennen wollen. Sie könnten Zahlen wohl oder übel in das Polynom einfügen und auf das Beste hoffen. Aber wie Sie gelernt haben, als Sie die quadratische Formel studiert haben, sind Nullen oft sehr unordentliche Zahlen; Zufälliges Raten ist wahrscheinlich nicht der beste Angriffsplan. Wie geht man also vor, Nullen zu finden?

Der Rational Roots (oder Rational Zeroes) – Test ist eine praktische Möglichkeit, eine Liste nützlicher erster Vermutungen zu erhalten, wenn Sie versuchen, die Nullen (Wurzeln) eines Polynoms zu finden., Bei einem Polynom mit ganzzahligen (dh positiven und negativen „Ganzzahl“-Koeffizienten) Koeffizienten werden die möglichen (oder potentiellen) Nullen gefunden, indem die Faktoren des konstanten (letzten) Terms über die Faktoren des führenden Koeffizienten aufgelistet werden, wodurch eine Liste von Brüchen gebildet wird. Diese Auflistung gibt Ihnen eine Liste potenzieller rationaler (gebrochener) Wurzeln zum Testen-daher der Name des Tests.

Lassen Sie mich betonen: Der Rational Roots Test gibt Ihnen nicht die Nullen. Es sagt nicht, was die Nullen definitiv sein werden., Der Test gibt Ihnen nur eine Liste von relativ einfachen und“ schönen “ Zahlen, die Sie im Polynom ausprobieren können. Die meisten dieser möglichen Nullen werden sich nicht wirklich als Nullen herausstellen!

Sie können den Sinn der Testmethodik sehen, indem Sie ein einfaches Polynom betrachten. Angesichts der quadratischen 12×2-7x-10 können Sie die quadratische Formel verwenden, um die Nullen zu finden, aber Sie können auch Faktor 12×2 – 7x – 10 = (3x + 2)(4x – 5). Wenn Sie die beiden Faktoren gleich Null setzen, erhalten Sie zwei Wurzeln bei x = – 2/3 und x = 5/4., Beachten Sie, dass die Nenner „3“ und „4“ Faktoren des führenden Koeffizienten „12“ sind und die Zähler „2“ und „5“ Faktoren des konstanten Terms „10“sind. Das heißt, die Nullen sind Brüche, die aus Faktoren des konstanten Terms (10) über Faktoren des führenden Koeffizienten (12) gebildet werden. Beachten Sie jedoch auch, dass Brüche wie 5/6 und – 10/3 auch auf diese Weise gebildet werden können (und Ihnen somit durch den Test zur Verfügung gestellt werden), aber diese anderen Brüche sind in der Tat keine Nullen dieses Quadrats.,

Diese Beziehung ist immer wahr: Wenn ein Polynom rationale Wurzeln hat, dann sind diese Wurzeln Brüche der Form (Plus-oder-Minus) (Faktor des konstanten Terms) / (Faktor des führenden Koeffizienten). Allerdings sind nicht alle Brüche dieser Form notwendigerweise Nullen des Polynoms. In der Tat kann es vorkommen, dass keiner der so gebildeten Brüche tatsächlich eine Null des Polynoms ist.

Beachten Sie, dass ich immer wieder“ potenzielle „Wurzeln,“ mögliche „Nullen“ sage, wenn es solche Wurzeln gibt…“., Dies liegt daran, dass die Liste der durch den Rational Roots-Test generierten Fraktionen nur eine Liste potenzieller Lösungen ist. Es muss nicht wahr sein, dass eine der Fraktionen tatsächlich eine Lösung ist. Es könnte keine gebrochenen Wurzeln geben! Bei x2-2 ergeben die rationalen Wurzeltests beispielsweise die folgenden möglichen rationalen Nullen:

Aber Sie wissen bereits, dass:

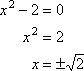
…die Nullen sind also überhaupt nicht rational.,

Denken Sie immer daran: Der Rational Roots Test gibt nur eine Liste von guten ersten Vermutungen; es gibt Ihnen NICHT“ die “ Antworten!

• Finden Sie alle möglichen rationalen x-Intercepts von x4 + 2×3-7×2-8x + 12.

Top | 1 | 2 | Return to Index Next >>