Kommutative, assoziative und distributive Gesetze
Wow! Was für ein Mund voll Worte! Aber die Ideen sind einfach.
Kommutative Gesetze
Die „kommutativen Gesetze“ besagen, dass wir Zahlen austauschen können und immer noch die gleiche Antwort erhalten …
… wenn wir hinzufügen:
a + b = b + a
Beispiel:
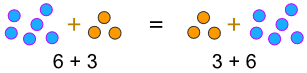
… oder, wenn wir multiplizieren:
a × b = b × a
Beispiel:
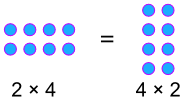
Kommutativen Prozentsätze!,
Weil a × b = b × a es ist auch wahr, dass a% von b = b% von a
Beispiel: 8% von 50 = 50% von 8, das ist 4

Warum“ kommutativ“… ?
Weil die Zahlen wie ein Pendler hin und her reisen können.
Assoziative Gesetze
Die“ Assoziativen Gesetze “ sagen, dass es egal ist, wie wir die Zahlen gruppieren (dh welche wir zuerst berechnen) …
…, wenn wir hinzufügen:
(a + b) + c = a + (b + c)
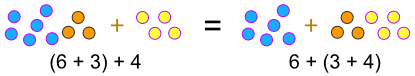
…,r>
| Dies: | (3 × 4) × 5 = 12 × 5 = 60 |
| Hat die gleiche Antwort wie diese: | 3 × (4 × 5) = 3 × 20 = 60 |
Verwendet:
Manchmal ist es einfacher, in einer anderen Reihenfolge hinzuzufügen oder zu multiplizieren:
Was ist 19 + 36 + 4?,
19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59
, Oder neu anordnen, ein wenig:
Was ist 2 × 16 × 5?
2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160
Verteilungsgesetz
Das „Verteilungsgesetz“ ist das BESTE von allen, muss aber sorgfältig beachtet werden.,
Dies ist, was es uns tun lässt:
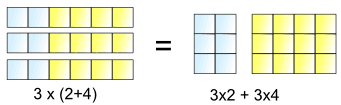
3 Lose (2+4) ist das gleiche wie 3 Lose von 2 plus 3 Lose von 4
So können die 3× über die 2+4 „verteilt“ werden, in 3×2 und 3×4
Und wir schreiben es so:
a × (b + c) = a × b + a × c
Versuchen Sie die Berechnungen selbst:
- 3 × (2 + 4) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
So oder so bekommt die gleiche Antwort.,
Auf Englisch können wir sagen:
Wir bekommen die gleiche Antwort, wenn wir:
- Multiplizieren Sie eine Zahl mit einer Gruppe von addierten Zahlen oder
- multiplizieren Sie sie einzeln und fügen Sie sie dann hinzu
Verwendet:
Manchmal ist es einfacher, eine schwierige Multiplikation aufzubrechen:
Beispiel: Was ist 6 × 204 ?
6 × 204 = 6×200 + 6×4
= 1,200 + 24
= jeweils 1.224
Oder kombinieren Sie:
Beispiel: Was ist 16 × 6 + 16 × 4?,
16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160
Wir können es auch in der Subtraktion verwenden:
Example: 26×3 – 24×3
= 2 × 3
= 6
Wir könnten es auch für eine lange Liste von Ergänzungen verwenden:
Example: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140
. . . aber geh nicht zu weit!,
Das Kommutative Gesetz funktioniert nicht für Subtraktion oder Division:
Beispiel:
- 12 / 3 = 4, aber
- 3 / 12 = ¼
Das assoziative Gesetz funktioniert nicht für Subtraktion oder Division:















