Laminare und turbulente Strömung

Die Eigenschaften der laminaren und turbulenten Strömung sind sehr unterschiedlich. Um zu verstehen, warum eine turbulente oder laminare Strömung im Betrieb eines bestimmten Systems wünschenswert ist, müssen die Eigenschaften einer laminaren und turbulenten Strömung verstanden werden.,

Strömungsregime

Der gesamte Fluidfluss wird in eine von zwei großen Kategorien oder Regimen eingeteilt. Diese beiden Strömungsregime sind laminare Strömung und turbulente Strömung. Das Strömungsregime, ob laminar oder turbulent, ist wichtig für die Konstruktion und den Betrieb eines Fluidsystems. Die Menge der Flüssigkeitsreibung, die die Energiemenge bestimmt, die zur Aufrechterhaltung des gewünschten Flusses erforderlich ist, hängt von der Strömungsart ab. Dies ist auch eine wichtige Überlegung in bestimmten Anwendungen, die Wärmeübertragung auf die Flüssigkeit beinhalten.,

Laminare Strömung

Laminare Strömung wird auch als streamline oder viskose Strömung bezeichnet. Diese Begriffe sind deskriptiv für die Strömung, da bei laminarer Strömung (1) Wasserschichten, die mit unterschiedlichen Geschwindigkeiten praktisch ohne Vermischung zwischen Schichten übereinander fließen, (2) Fluidpartikel sich auf bestimmten und beobachtbaren Wegen oder Stromlinien bewegen und (3) die Strömung charakteristisch für viskose (dicke) Flüssigkeit ist oder eine, bei der die Viskosität der Flüssigkeit eine bedeutende Rolle spielt.

Turbulente Strömung

Turbulente Strömung ist durch die unregelmäßige Bewegung von Partikeln der Flüssigkeit gekennzeichnet., Es gibt keine bestimmte Frequenz wie in Wellenbewegung. Die Partikel bewegen sich auf unregelmäßigen Wegen ohne beobachtbares Muster und ohne bestimmte Schichten.

Strömungsgeschwindigkeitsprofile

Nicht alle Fluidpartikel bewegen sich mit der gleichen Geschwindigkeit innerhalb eines Rohres. Die Form der Geschwindigkeitskurve (das Geschwindigkeitsprofil über einen bestimmten Abschnitt des Rohrs) hängt davon ab, ob die Strömung laminar oder turbulent ist. Wenn die Strömung in einem Rohr laminar ist, ist die Geschwindigkeitsverteilung bei einem Querschnitt parabolisch, wobei die maximale Geschwindigkeit in der Mitte etwa doppelt so hoch ist wie die durchschnittliche Geschwindigkeit in dem Rohr., Bei turbulenter Strömung besteht eine ziemlich flache Geschwindigkeitsverteilung über den Rohrabschnitt, mit dem Ergebnis, dass das gesamte Fluid mit einem bestimmten Wert fließt. Abbildung 5 hilft, die obigen Ideen zu veranschaulichen. Die Geschwindigkeit des Fluids in Kontakt mit der Rohrwand ist im Wesentlichen Null und erhöht sich je weiter von der Wand entfernt.

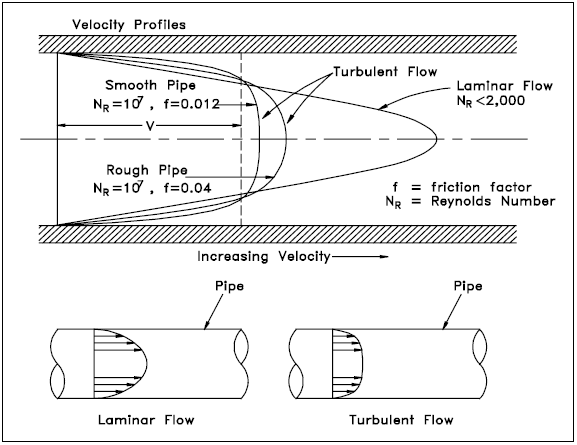
Hinweis aus Abbildung 5, dass das Geschwindigkeitsprofil vom Oberflächenzustand der Rohrwand abhängt., Eine glattere Wand führt zu einem gleichmäßigeren Geschwindigkeitsprofil als eine raue Rohrwand.

Durchschnittliche (Massen -) Geschwindigkeit

Bei vielen Fluidströmungsproblemen reicht es aus, anstatt genaue Geschwindigkeiten an verschiedenen Stellen im selben Strömungsquerschnitt zu bestimmen, eine einzige Durchschnittsgeschwindigkeit zuzulassen, um die Geschwindigkeit des gesamten Fluids an diesem Punkt im Rohr darzustellen. Dies ist für turbulente Strömungen ziemlich einfach, da das Geschwindigkeitsprofil über den größten Teil des Rohrquerschnitts flach ist. Es ist vernünftig anzunehmen, dass die Durchschnittsgeschwindigkeit der Geschwindigkeit in der Mitte des Rohrs entspricht.,

Wenn das Strömungsregime laminar ist (das Geschwindigkeitsprofil ist parabolisch), besteht immer noch das Problem, die „durchschnittliche“ Geschwindigkeit bei einem bestimmten Querschnitt darzustellen, da in den Fluidströmungsgleichungen ein Durchschnittswert verwendet wird. Technisch geschieht dies mittels Integralrechnung. Praktisch sollte der Schüler einen Durchschnittswert verwenden, der die Hälfte des Mittellinienwerts beträgt.

Viskosität

Viskosität ist eine Fluideigenschaft, die den Widerstand des Fluids gegen Verformung aufgrund einer Scherkraft misst., Viskosität ist die innere Reibung eines Fluids, die es widerstandsfähig macht, an einer festen Oberfläche oder anderen Schichten des Fluids vorbeizufließen. Die Viskosität kann auch als Maß für den Widerstand einer Flüssigkeit gegen das Fließen angesehen werden. Ein dickes Öl hat eine hohe Viskosität; Wasser hat eine niedrige Viskosität. Die Maßeinheit für die absolute Viskosität ist:

Die Viskosität eines Fluids ist üblicherweise signifikant von der Temperatur des Fluids abhängig und relativ unabhängig vom Druck., Bei den meisten Flüssigkeiten nimmt die Viskosität des Fluids ab, wenn die Temperatur des Fluids ansteigt. Ein Beispiel dafür ist das Schmieröl von Motoren. Wenn der Motor und sein Schmieröl kalt sind, ist das Öl sehr viskos oder dick. Nach dem Starten des Motors und dem Temperaturanstieg des Schmieröls nimmt die Viskosität des Öls erheblich ab und das Öl scheint viel dünner zu sein.

Ideale Flüssigkeit

Eine ideale Flüssigkeit ist inkompressibel und hat keine Viskosität., Ideale Flüssigkeiten existieren eigentlich nicht, aber manchmal ist es nützlich zu überlegen, was mit einer idealen Flüssigkeit in einem bestimmten Flüssigkeitsströmungsproblem passieren würde, um das Problem zu vereinfachen.

Reynoldszahl

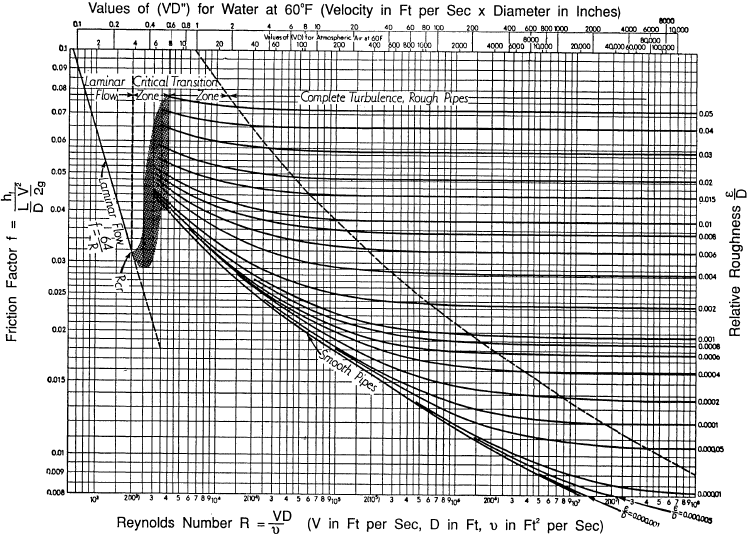
Das Strömungsregime (entweder laminar oder turbulent) wird durch Auswertung der Reynoldszahl der Strömung bestimmt (siehe Abbildung 5). Die Reynolds-Zahl, basierend auf Studien von Osborn Reynolds, ist eine dimensionslose Zahl, die aus den physikalischen Eigenschaften der Strömung besteht. Gleichung 3-7 wird verwendet, um die Reynolds-Zahl (NR) für den Fluidfluss zu berechnen.,

wobei:

Wenn die Reynolds-Zahl für praktische Zwecke kleiner als 2000 ist, ist der Fluss laminar. Wenn es größer als 3500 ist, ist die Strömung turbulent. Ströme mit Reynolds-Zahlen zwischen 2000 und 3500 werden manchmal als Übergangsströme bezeichnet. Die meisten Fluidsysteme in Kernanlagen arbeiten mit turbulenter Strömung. Reynolds-Zahlen können bequem mit einem launischen Diagramm bestimmt werden, von dem ein Beispiel unten gezeigt wird. Weitere Details zur Verwendung des Stimmungsdiagramms finden Sie im nachfolgenden Text.,