de façon très informelle, les deux termes de la somme donnée par la formule de Black-Scholes peuvent être considérés comme « le cours actuel de l’action pondéré par la probabilité que vous exercerez votre option d’achat de l’action « moins » le prix réduit de l’exercice de l’option pondéré par la probabilité que vous exercerez l’option », ou simplement « ce que vous allez obtenir « moins » ce que vous allez payer  » (Khan, 2013).,

pour une option de vente européenne (contrats pour le droit, mais pas l’obligation, de vendre un actif sous-jacent à un prix prédéterminé à une date prédéterminée à l’avenir), la forme fonctionnelle équivalente est:

exemple: calcul du prix d’une option D’achat européenne

pour calculer le prix d’une option D’achat européenne, nous savons que nous avons besoin de cinq valeurs requises par l’équation 6 ci-dessus. Ils sont: 1. Le cours actuel des actions, 2. Le prix d’exercice de l’option d’achat (X), 3. Le délai d’expiration (T – t), 4. Le taux d’intérêt sans risque (r) et 5., La volatilité du stock, donnée par l’écart-type des rendements logarithmiques historiques (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

Nous pouvons estimer la volatilité de n’importe quelle action en observant ses prix historiques, ou, encore plus simple, en calculant d’autres prix d’option pour la même action à des dates d’échéance/d’expiration différentes (T) et des prix d’exercice / d’exercice (X), si nous savons qu’ils ont été La valeur résultante, σ, est un nombre compris entre 0 et 1, représentant la volatilité implicite du marché pour l’action., Pour Tesla, au moment de la rédaction de cet article, la valeur moyenne était d’environ 0.38 pour 4-5 prix d’options différents autour de la même date d’expiration/échéance. En entrant dans l’équation 6 ci-dessus, nous constatons que l’option d’achat qui nous intéresse devrait être des prix autour de 7$.

volatilité implicite

bien qu’il soit intéressant de comprendre comment les émetteurs d’options arrivent au prix de leurs options d’achat et de vente, en tant qu’investisseurs, il est difficile de « ne pas être d’accord” avec de tels prix, en soi, et donc difficile de transformer ces connaissances en thèses d’investissement exploitables.,

Nous pouvons cependant obtenir beaucoup de kilométrage de la formule de Black-Scholes si nous traitons plutôt le prix d’une option (C ou P) comme une quantité connue/variable indépendante (trouvée en regardant différentes dates de maturité/expiration T et différents prix D’exercice X). Ceci parce que, si nous le faisons, L’équation fonctionnelle de Black-Scholes devient un outil pour nous aider à comprendre comment le marché estime la volatilité d’une action, également connue sous le nom de volatilité implicite de l’option. Ce sont des informations sur lesquelles nous pouvons être en désaccord et contre lesquelles nous échangeons.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called « continuous timeline instruments”), they are much more difficult to deal with that European options (« point in time instruments”)., Principalement, étant donné que la Politique d’exercice optimal affectera la valeur de l’option, cela doit être pris en compte lors de la résolution de L’équation aux Dérivées Partielles de Black-Scholes. Il n’existe pas de solutions « fermées” connues pour les options américaines selon L’équation de Black-Scholes. Il existe cependant quelques cas particuliers:

• Pour les options D’achat américaines sur des actifs sous-jacents qui ne paient pas de dividende (ou d’autres paiements), le prix des options D’achat américaines est le même que pour les options D’achat européennes. Ceci parce que la Politique d’exercice optimale dans ce cas est de ne pas exercer l’option.,
• Pour les options D’achat américaines sur des actifs sous-jacents qui versent un dividende connu au cours de leur vie, il peut être optimal d’exercer l’option tôt., Dans de tels cas, l’option peut être exercée de manière optimale juste avant que l’action ne passe hors dividende, selon une solution donnée sous forme fermée par la méthode dite de Roll-Geske-Whaley (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

Vérifiez D’abord s’il est optimal d’exercer l’option tôt, en examinant si l’inégalité suivante est remplie:

pour S = cours de l’action, X = prix d’exercice, D₁ = dividende versé, t = date actuelle, t₁ = date de paiement du dividende, T = date d’expiration de l’option.

Si l’inégalité n’est pas remplie, l’exercice précoce n’est pas optimal., Si C ( – ) est la formule normale de Black・ Scholes pour les options D’achat européennes sur des actions non payantes de dividendes (eq x), la valeur de l’option D’achat américaine est alors donnée par une version de la même équation où le cours de l’action est actualisé:

Si l’inégalité est satisfaite, au début de l’exercice est optimal et la valeur de l’American de l’option d’achat est donné par la suivante, horrible, désordre d’une équation (j’ai essayé de le casser en place par chaque terme pour le rendre plus lisible):

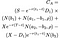
où comme précédemment S = prix de l’Action, T = date d’expiration de l’option, X = prix d’exercice et r = taux d’intérêt sans risque, σ = volatilité (écart type du log des rendements historiques de l’action), et D₁ est le paiement du dividende. En outre, ρ est donnée par:

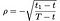
a₁, a₂ by:

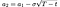
and b₁, b₂ by:

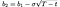
Limitations

Il va sans dire que le modèle Black-Scholes est précisément cela, un modèle théorique qui tente d’estimer le comportement d’un marché, compte tenu des hypothèses énoncées ci-dessus et des limites inhérentes à nos propres estimations numériques des taux d’intérêt sans risque (r) et de la volatilité future (σ). Il convient ici de souligner que toutes les hypothèses de (en particulier le modèle original) ne sont en fait pas valables empiriquement., Par exemple, des limites importantes découlent de:

• la sous-estimation des mouvements extrêmes de l’action, le rendement du risque de queue
• l’hypothèse d’une négociation instantanée et sans coût, le rendement du risque de liquidité
• l’hypothèse d’un processus stationnaire, le rendement du risque de volatilité
• l’hypothèse d’un temps et d’une négociation continus, le rendement du risque de gap

options, négociation sur plusieurs bourses, couverture avec couverture de volatilité et couverture gamma, respectivement.,

contexte

comme brièvement mentionné, ce sont Fischer Black et Myron Scholes qui, en 1973, ont montré que la révision dynamique d’un portefeuille selon certaines règles supprime le rendement attendu du titre sous-jacent (Black& Scholes, 1973). Leur modèle s’appuie sur des travaux déjà établis de Bachelier, Samuelson et d’autres. Robert C. Merton a été le premier à publier un article développant la compréhension du modèle et qui a inventé le terme « modèle de tarification des options Black-Scholes”., Scholes et Merton ont reçu le prix Nobel de sciences économiques en 1997 pour leur découverte de la méthode de séparation des options d’achat d’actions du risque de leurs titres sous-jacents. Comme Fischer Black est décédé en 1995, il ne serait pas admissible à recevoir le prix, mais a été reconnu comme un contributeur par L’Académie Nobel.