Retour à l’Index des Leçons | Faire les Leçons dans l’Ordre | imprimable de la page

Le Rationnel Racines Test: Introduction (page 1 de 2)

Le zéro d’un polynôme est une valeur d’entrée (généralement une valeur x) qui retourne une valeur de zéro pour l’ensemble du polynôme lorsque vous le branchez dans le polynôme. Quand un Zéro est un nombre réel (c’est-à-dire non complexe), c’est aussi une ordonnée à l’origine du Graphe de la fonction polynomiale., Vous voudrez souvent (surtout en calcul) connaître l’emplacement des zéros d’une fonction polynomiale donnée. Vous pouvez brancher des nombres dans le polynôme, bon gré mal gré, et espérer le meilleur. Mais comme vous l’avez appris lorsque vous avez étudié la formule quadratique, les zéros sont souvent des nombres très désordonnés; deviner au hasard n’est probablement pas le meilleur plan d’attaque. Alors, comment va-t-on essayer de trouver des zéros?

Le test des racines Rationnelles (ou zéros rationnels) est un moyen pratique d’obtenir une liste de premières suppositions utiles lorsque vous essayez de trouver les zéros (racines) d’un polynôme., Étant donné un polynôme à coefficients entiers (c’est-à-dire positifs et négatifs « nombre entier »), les zéros possibles (ou potentiels) sont trouvés en énumérant les facteurs du (dernier) terme constant sur les facteurs du coefficient principal, formant ainsi une liste de fractions. Cette liste vous donne une liste de racines rationnelles (fractionnaires) potentielles à tester-d’où le nom du Test.

permettez-moi de souligner: le Test des racines rationnelles ne vous donne pas les zéros. Il ne dit pas ce que seront définitivement les zéros., Le Test ne vous donne qu’une liste de nombres relativement faciles et « gentils » à essayer dans le polynôme. La plupart de ces zéros possibles ne seront pas réellement des zéros!

Vous pouvez voir le sens de la méthodologie du Test en regardant un polynôme simple. Étant donné le quadratique 12×2 – 7x – 10, vous pouvez utiliser la formule quadratique pour trouver les zéros, mais vous pouvez également factoriser pour obtenir 12×2 – 7x – 10 = (3x + 2)(4x-5). Réglage de la deux facteurs égaux à zéro, vous obtenez deux racines x = – 2/3 et x = 5/4., Notez que les dénominateurs « 3 » et « 4 » sont des facteurs du coefficient principal « 12 », et les numérateurs « 2 » et « 5 »sont des facteurs du terme constant « 10 ». C’est-à-dire que les zéros sont des fractions formées de facteurs du terme constant (10) sur des facteurs du coefficient principal (12). Notez également, cependant, que des fractions telles que 5/6 et – 10/3 peuvent également être formées de cette façon (et donc vous être fournies par le Test), mais ces autres fractions ne sont pas en fait des zéros de ce quadratique.,

cette relation est toujours vraie: si un polynôme a des racines rationnelles, alors ces racines seront des fractions de la forme (plus ou moins) (facteur du terme constant) / (facteur du coefficient principal). Cependant, toutes les fractions de cette forme ne sont pas nécessairement des zéros du polynôme. En effet, il peut arriver qu’aucune des fractions ainsi formées ne soit en fait un zéro du polynôme.

Notez que je ne cesse de dire « potentiel » causes », « possible » zéros, « s’il y a des racines… »., En effet, la liste des fractions générées par le Test Rational Roots n’est qu’une liste de solutions potentielles. Il n’est pas nécessaire que l’une des fractions soit en fait une solution. Il pourrait ne pas y avoir de racines fractionnaires! Par exemple, étant donné x2 – 2, le Rationnel Racines Tests donne rationnelle possible des zéros:

Mais vous savez déjà que:

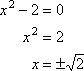
…donc les zéros ne sont pas réellement rationnelle à tous.,

rappelez-vous toujours: le test des racines rationnelles ne donne qu’une liste de bonnes premières suppositions; il ne vous donne pas « les » réponses!

• Trouvez toutes les interceptions x rationnelles possibles de x4 + 2×3-7×2 – 8x + 12.

Top | 1 | 2 | Return to Index Next >>