Lois commutatives, associatives et distributives
Wow! Quelle bouchée de mots! Mais les idées sont simples.
lois commutatives
les « lois commutatives » disent que nous pouvons échanger des nombres et obtenir toujours la même réponse …
… quand on ajoute:
a + b = b + a
Exemple:
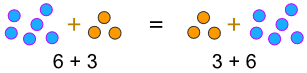
… ou quand nous multiplions:
a × b = b × a
Exemple:
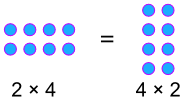
Commutative Pourcentages!,
Parce que a × b = b × a, il est vrai aussi qu’un% de b = b,% de un
Exemple: 8% de 50 = 50% de 8, qui est 4

Pourquoi « commutative » … ?
parce que les chiffres peuvent voyager d’avant en arrière comme un banlieusard.
lois associatives
les « lois associatives » disent que peu importe comment nous regroupons les nombres (c’est-à-dire que nous calculons en premier) …
…, quand on ajoute:
(a + b) + c = a + (b + c)
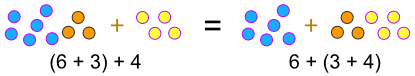
…,r>
| Ceci: | (3 × 4) × 5 = 12 × 5 = 60 |
| A la même réponse, comme ceci: | 3 × (4 × 5) = 3 × 20 = 60 |
Utilisation:
Parfois, il est plus facile d’ajouter ou multiplier dans un ordre différent:
qu’est-Ce que 19 + 36 + 4?,
19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59
Ou de réorganiser un peu:
qu’est-Ce que 2 × 16 × 5?
2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160
Loi de Distributivité
La « Loi de Distributivité » est le MEILLEUR de tous, mais il a besoin d’une attention minutieuse.,
c’est Ce qu’il nous permet de faire:
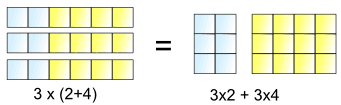
3 lots de (2+4) est le même que 3 lots de 2 plus 3 lots de 4
Donc, le 3× peut être « distribué » à travers l’2+4, en 3×2 et 3×4
Et, nous l’écrire comme ceci:
a × (b + c) = a × b + a × c
Essayez le calcul vous-même:
- 3 × (2 + 4) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
de toute façon obtient la même réponse.,
En anglais, nous pouvons dire:
Nous obtenir la même réponse quand nous avons:
- multiplier un nombre par un groupe de numéros additionnés, ou
- faire chaque multiplier séparément, puis les ajouter
Utilise:
Parfois, il est plus facile de briser un difficile de multiplication:
Exemple: qu’est-Ce que 6 × 204 ?
6 × 204 = 6×200 + 6×4
= de 1 200 + 24
= 1,224
Ou à combiner:
Exemple: qu’est-Ce que 16 × 6 + 16 × 4?,
16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160
On peut l’utiliser dans la soustraction trop:
Exemple: 26×3 – 24×3
= 2 × 3
= 6
Nous avons pu l’utiliser pendant une longue liste d’ajouts, trop:
Exemple: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140
. . . mais n’allez pas trop loin!,
La Loi Commutative ne fonctionne pas pour la soustraction ou division:
Exemple:
- 12 / 3 = 4, mais
- 3 / 12 = ¼
L’Associatif Loi ne fonctionne pas pour la soustraction ou division:















