wanneer een vrije positieve lading q wordt versneld door een elektrisch veld wordt het kinetische energie gegeven (figuur \(\paginindex{1}\))., Het proces is analoog aan een voorwerp dat wordt versneld door een zwaartekrachtveld, alsof de lading een elektrische heuvel afdaalt waar zijn elektrische potentiële energie wordt omgezet in kinetische energie, hoewel de bronnen van de krachten natuurlijk heel verschillend zijn. Laten we het werk van een lading q door het elektrische veld in dit proces onderzoeken, zodat we een definitie van elektrische potentiële energie kunnen ontwikkelen.

De elektrostatische of Coulomb-kracht is conservatief, wat betekent dat het werk aan q onafhankelijk is van het gekozen pad, zoals we later zullen aantonen., Dit is precies analoog aan de zwaartekracht. Wanneer een kracht conservatief is, is het mogelijk om een potentiële energie te definiëren die geassocieerd is met de kracht. Het is meestal gemakkelijker om te werken met de potentiële energie (omdat het alleen afhangt van de positie) dan om het werk direct te berekenen.

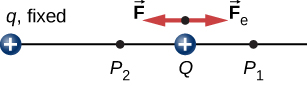
het werk \(W_{12}\) gedaan door de toegepaste kracht \(\vec{F}\) wanneer het deeltje beweegt van \(P_1\) naar \(P_2\) kan worden berekend door

\

\

waar we positief hebben gedefinieerd om weg te wijzen van de oorsprong en r is de afstand van de oorsprong. De richtingen van zowel de verplaatsing als de uitgeoefende kracht in het systeem in Figuur \(\Paginindex{2}\) zijn parallel, en dus is het werk aan het systeem positief.

we gebruiken de letter U om elektrische potentiële energie aan te duiden, die eenheden van Joule (J) heeft., Wanneer een conservatieve kracht negatief werk doet, wint het systeem potentiële energie. Wanneer een conservatieve kracht positief werk doet, verliest het systeem potentiële energie, \(\Delta U = – W\). In het systeem in Figuur \(\Paginindex{3}\) werkt de Coulomb-kracht in de tegenovergestelde richting van de verplaatsing; daarom is het werk negatief. We hebben echter de potentiële energie in het tweelastsysteem verhoogd.

in dit voorbeeld is het werk W gedaan om een positieve lading uit rust te versnellen positief en het resultaat van een verlies in U, of een negatief \(\Delta U\)., Een waarde voor U kan op elk punt worden gevonden door het ene punt als referentie te nemen en het werk te berekenen dat nodig is om een lading naar het andere punt te verplaatsen.

Gravitatiepotentiaalenergie en elektrische potentiaalenergie zijn vrij analoog. Potentiële energie is het werk van een conservatieve kracht en geeft extra inzicht over energie en energietransformatie zonder de noodzaak om direct met de kracht om te gaan. Het komt bijvoorbeeld veel vaker voor om het concept van elektrische potentiele energie te gebruiken dan om de Coulomb-kracht direct in reële toepassingen aan te pakken.,

\

merk op dat Q Een constante is.

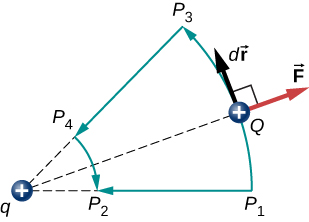
een andere implicatie is dat we een potentiële elektrische energie kunnen definiëren. Bedenk dat het werk van een conservatieve kracht ook wordt uitgedrukt als het verschil in de potentiële energie die overeenkomt met die kracht., Daarom kan het werk \(W_{ref}\) om een lading van een referentiepunt naar een interessant punt te brengen worden geschreven als

\

en, door vergelijking \ref{7.1}, is het verschil in potentiële energie (\(u_2 – U_1\)) van de testlading Q tussen de twee punten

daarom kunnen we een algemene uitdrukking schrijven voor de potentiële energie van twee puntladingen (in sferische coördinaten):

\_{r_{Ref}}^R = kqq\Left.,\]

We kunnen de tweede term gebruiken als een willekeurig constant referentieniveau, dat dient als nulreferentie:

\

een handige referentiekeuze die gebaseerd is op ons gezond verstand is dat wanneer de twee ladingen oneindig ver uit elkaar liggen, er geen interactie tussen hen is. (Herinneren aan de bespreking van referentie-potentiële energie in Potentiële Energie en behoud van energie.,) Als we de potentiële energie van deze toestand als nul nemen, wordt de term \(u_{ref}\) uit de vergelijking verwijderd (net als wanneer we zeggen dat de grond nul potentiële energie is in een gravitatiepotentiaalenergieprobleem), en de potentiële energie van Q wanneer deze wordt gescheiden van q door een afstand r neemt de vorm

\

als gevolg van Coulomb ‘ s wet, de krachten als gevolg van meerdere ladingen op een testlading \(Q\) Over; ze kunnen afzonderlijk worden berekend en vervolgens worden toegevoegd. Dit impliceert dat de werkintegralen en dus de resulterende potentiële energieën hetzelfde gedrag vertonen., Om dit aan te tonen, beschouwen we een voorbeeld van het samenstellen van een systeem van vier ladingen.

merk op dat de elektrische potentiaalenergie positief is als de twee ladingen van hetzelfde type zijn, positief of negatief, en negatief als de twee ladingen van tegengestelde types zijn. Dit is logisch als je denkt aan de verandering in de potentiële energie \(\Delta u\) als je de twee ladingen dichterbij brengt of verder uit elkaar beweegt., Afhankelijk van de relatieve soorten kosten, je kan hebben om te werken aan het systeem of het systeem zou werken op u, dat wil zeggen, uw werk is ofwel positief of negatief. Als je positief werk aan het systeem moet doen (eigenlijk de ladingen dichterbij duwen), dan moet de energie van het systeem toenemen. Als je twee positieve ladingen of twee negatieve ladingen dichterbij brengt, moet je positief werk doen aan het systeem, dat hun potentiële energie verhoogt. Aangezien de potentiële energie evenredig is aan 1 / r, stijgt de potentiële energie wanneer r daalt tussen twee positieve of twee negatieve ladingen.,

aan de andere kant, als je een positieve en een negatieve lading dichterbij brengt, moet je negatief werk doen aan het systeem (de ladingen trekken je aan), wat betekent dat je energie uit het systeem haalt. Dit vermindert de potentiële energie. Aangezien potentiële energie negatief is in het geval van een positief en een negatief ladingspaar, maakt de toename in 1/r de potentiële energie negatiever, wat hetzelfde is als een vermindering van potentiële energie.

het resultaat van voorbeeld \(\Paginindex{2}\) kan worden uitgebreid tot systemen met een willekeurig aantal kosten., In dit geval is het het meest handig om de formule te schrijven als

\

de factor 1/2 zorgt voor het twee keer optellen van elk paar ladingen.