Commutatieve, associatieve en distributieve wetten
Wow! Wat een mond vol woorden! Maar de ideeën zijn simpel.
commutatieve wetten
de “commutatieve wetten” zeggen dat we getallen kunnen verwisselen en toch hetzelfde antwoord krijgen …
… wanneer we toevoegen:
a + b = b + a
voorbeeld:
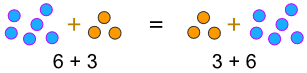
… of wanneer we vermenigvuldigen:
a × b = b × a
voorbeeld:
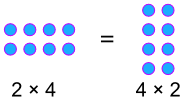
commutatieve Percentages!,
omdat A × b = b × a Het is ook waar dat A% van b = B% van a
Voorbeeld: 8% van 50 = 50% van 8, dat is 4

waarom “commutatief” … ?
omdat de getallen heen en weer kunnen reizen als een forens.
associatieve wetten
de” associatieve wetten ” zeggen dat het niet uitmaakt hoe we de getallen groeperen (dat wil zeggen welke we als eerste berekenen) …
…, wanneer we toevoegen:
(a + b) + c = a + (b + c)
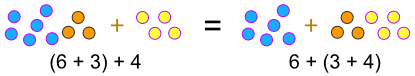
…,r>
| Is: | (3 × 4) × 5 = 12 × 5 = 60 |
| Heeft hetzelfde antwoord als volgt op: | 3 × (4 × 5) = 3 × 20 = 60 |
Gebruik:
Soms is het makkelijker om toe te voegen of te vermenigvuldigen in een andere volgorde:
Wat is 19 + 36 + 4?,
19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59
of een beetje herschikken:
Wat is 2 × 16 × 5?
2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160
distributieve wet
de “distributieve wet” is de beste van allemaal, maar verdient zorgvuldige aandacht.,
Dit is wat het ons laat doen:
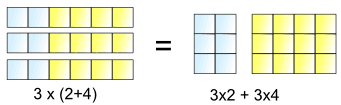
3 partijen (2+4) is dezelfde als die 3 partijen van 2 en 3 veel 4
Dus, het 3× kunnen worden “verdeeld” over de 2+4, in 3×2 en 3×4
En we schrijven dit als volgt:
a × (b + c) = a × b + a × c
Probeer de berekeningen zelf uit:
- 3 × (2 + 4) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
een van Beide manier krijgt het zelfde antwoord.,
In het Engels kunnen we zeggen:
we krijgen hetzelfde antwoord als we:
- vermenigvuldig een getal met een groep getallen die bij elkaar worden opgeteld, of
- vermenigvuldig elk afzonderlijk en voeg ze toe
gebruikt:
soms is het makkelijker om een moeilijke vermenigvuldiging op te breken:
voorbeeld: Wat is 6 × 204 ?
6 × 204 = 6×200 + 6×4
= 1,200 + 24
= 1,224
of te combineren:
voorbeeld: wat is 16 × 6 + 16 × 4?,
16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160
We kunnen het gebruiken in aftrekken ook:
Voorbeeld: 26×3 – 24×3
= 2 × 3
= 6
We kunnen gebruiken voor een lange lijst van toevoegingen, ook:
Voorbeeld: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140
. . . maar ga niet te ver!,
de commutatieve wet werkt niet voor aftrekking of deling:
voorbeeld:
- 12 / 3 = 4, maar
- 3 / 12 = ¼
de associatieve wet werkt niet voor aftrekking of deling:















