terugkeer naar de Lessons Index/doe de lessen in volgorde | Printvriendelijke pagina<| p>

De Rational Roots Test: Introduction (page 1 of 2)

de nulwaarde van een veelterm is een invoerwaarde (meestal een X-waarde) die een waarde van nul voor de hele polynoom retourneert wanneer je deze in de polynoom plug. Wanneer een nul een reëel (dat wil zeggen, niet complex) getal is, is het ook een X-ordinaat van de grafiek van de veeltermfunctie., U zult vaak (vooral in calculus) de locatie van de nullen van een bepaalde veeltermfunctie willen weten. Je zou nummers in de polynoom kunnen stoppen, willens en wetens, en hopen op het beste. Maar zoals je leerde toen je de kwadratische formule bestudeerde, zijn nullen vaak zeer rommelige getallen; willekeurig raden is waarschijnlijk niet het beste aanvalsplan. Dus hoe gaat men op zoek naar nullen?

De Rational Roots (of Rational nullen) Test is een handige manier om een lijst van nuttige eerste gissingen te verkrijgen wanneer je probeert de nullen (wortels) van een veelterm te vinden., Gegeven een veelterm met geheel getal (dat wil zeggen, positieve en negatieve “geheel getal”) coëfficiënten, worden de mogelijke (of potentiële) nullen gevonden door de factoren van de constante (laatste) term over de factoren van de leidende coëfficiënt op te sommen, waardoor een lijst van fracties wordt gevormd. Deze lijst geeft je een lijst van mogelijke rationele (fractionele) wortels om te testen-vandaar de naam van de Test.

laat me benadrukken: de Rational Roots Test geeft je niet de nullen. Het zegt niet wat de nullen zeker zullen zijn., De Test geeft je alleen een lijst van relatief eenvoudige en” mooie ” getallen om te proberen in de veelterm. De meeste van deze mogelijke nullen blijken niet echt nullen te zijn!

u kunt de Betekenis van de methode van de Test zien door te kijken naar een eenvoudige veelterm. Gegeven de kwadratische 12×2 – 7x-10, kunt u de kwadratische formule gebruiken om de nullen te vinden, maar u kunt ook factor 12×2 – 7x – 10 = (3x + 2)(4x – 5). Stel de twee factoren gelijk aan nul, dan krijg je twee wortels op x = – 2/3 en x = 5/4., Merk op dat de noemers “3” en “4” factoren zijn van de leidende coëfficiënt “12”, en de tellers “2” en “5” factoren zijn van de constante term “10”. Dat wil zeggen, de nullen zijn fracties gevormd van factoren van de constante term (10) over factoren van de leidende coëfficiënt (12). Merk echter ook op dat breuken zoals 5/6 en-10/3 ook op deze manier kunnen worden gevormd (en dus door de Test aan u worden verstrekt), maar deze andere breuken zijn in feite geen nullen van deze kwadratische.,

Deze relatie is altijd waar: als een veelterm rationale wortels heeft, dan zijn die wortels fracties van de vorm (plus-of-minus) (factor van de constante term) / (factor van de leidende coëfficiënt). Echter, niet alle fracties van deze vorm zijn noodzakelijkerwijs nullen van de veelterm. Inderdaad, het kan gebeuren dat geen van de aldus gevormde fracties eigenlijk een nul van de veelterm is.

advertentie

merk op dat ik blijf zeggen” potentiële “wortels,” mogelijke “nullen,” als er dergelijke wortels…”., Dit komt omdat de lijst van fracties gegenereerd door de Rational Roots Test is slechts een lijst van mogelijke oplossingen. Het hoeft niet waar te zijn dat een van de fracties eigenlijk een oplossing is. Misschien zijn er geen fractionele wortels! Bijvoorbeeld, gegeven x2-2, geeft de Rational Roots Tests de volgende mogelijke rationale nullen:

maar u weet al dat:

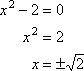
…dus de nullen zijn helemaal niet rationeel.,

onthoud altijd: de Rational Roots Test geeft alleen een lijst van goede eerste gissingen; het geeft je niet “de” antwoorden!

• Vind alle mogelijke rationele x-Onderscheppingen van x4 + 2×3-7×2-8x + 12.

u kunt een snelle grafiek maken (vooral als u een grafische rekenmachine hebt), en zien dat, uit de bovenstaande lijst, het waarschijnlijk goed zou zijn om te beginnen met zoeken naar nullen door de waarden x = -3, -2, 1 en 2 in de polynoom te steken.,

Top | 1 | 2 | Return to Index Next >>