Laminaire en Turbulente Stroming

De kenmerken van laminaire en turbulente stroming zijn zeer verschillend. Om te begrijpen waarom turbulente of laminaire stroming wenselijk is in de werking van een bepaald systeem, is het noodzakelijk om de kenmerken van laminaire en turbulente stroming te begrijpen.,

stroomschema ’s

alle vloeistofstromen worden ingedeeld in een van de twee grote categorieën of schema’ s. Deze twee stromingsregimes zijn laminaire stroming en turbulente stroming. Het stromingsregime, laminair of turbulent, is belangrijk bij het ontwerp en de werking van elk vloeistofsysteem. De hoeveelheid vloeistof wrijving, die de hoeveelheid energie die nodig is om de gewenste stroom te handhaven bepaalt, hangt af van de modus van de stroom. Dit is ook een belangrijke overweging in bepaalde toepassingen die warmteoverdracht naar de vloeistof te betrekken.,

laminaire stroom

laminaire stroom wordt ook wel stroomlijn of viskeuze stroom genoemd. Deze termen beschrijven de stroming omdat, in laminaire stroming, (1) lagen water die over elkaar stromen met verschillende snelheden en vrijwel geen vermenging tussen lagen, (2) vloeistof deeltjes bewegen in bepaalde en waarneembare paden of stroomlijnen, en (3) de stroming is kenmerkend voor viskeuze (dikke) vloeistof of is er een waarin de viscositeit van de vloeistof een belangrijke rol speelt.

turbulente stroom

turbulente stroom wordt gekenmerkt door de onregelmatige beweging van deeltjes van de vloeistof., Er is geen vaste frequentie zoals in golfbeweging. De deeltjes reizen in onregelmatige paden zonder waarneembaar patroon en zonder duidelijke lagen.

Stroomsnelheidsprofielen

niet alle vloeistofdeeltjes bewegen met dezelfde snelheid binnen een leiding. De vorm van de snelheidscurve (het snelheidsprofiel over een bepaald deel van de pijp) hangt af van de vraag of de stroom laminair of turbulent is. Als de stroom in een pijp laminair is, zal de snelheidsverdeling bij een dwarsdoorsnede parabolisch van vorm zijn met de maximale snelheid in het midden ongeveer tweemaal de gemiddelde snelheid in de pijp., Bij turbulente stroming bestaat er een vrij vlakke snelheidsverdeling over het leidinggedeelte, met als resultaat dat de gehele vloeistof bij een bepaalde waarde stroomt. Figuur 5 illustreert de bovenstaande ideeën. De snelheid van de vloeistof in contact met de buiswand is in wezen nul en neemt toe naarmate de wand verder weg is.

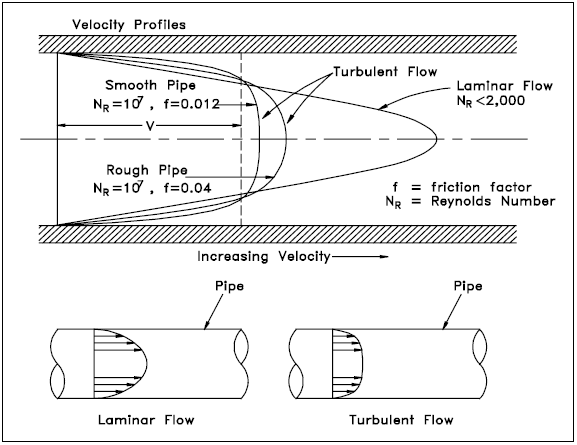
opmerking uit Figuur 5 dat het snelheidsprofiel afhankelijk is van de oppervlakteconditie van de buiswand., Een gladdere wand resulteert in een gelijkmatiger snelheidsprofiel dan een ruwe buiswand.

gemiddelde (Bulk) snelheid

In veel vloeistofstroomproblemen is het voldoende om, in plaats van de exacte snelheden op verschillende plaatsen in dezelfde stroomdoorsnede te bepalen, één enkele gemiddelde snelheid toe te staan om de snelheid van alle vloeistof op dat punt in de leiding weer te geven. Dit is vrij eenvoudig voor turbulente stroming omdat het snelheidsprofiel vlak is over het grootste deel van de pijpdoorsnede. Het is redelijk om aan te nemen dat de gemiddelde snelheid gelijk is aan de snelheid in het midden van de pijp.,

als het stroomschema laminair is (het snelheidsprofiel is parabool), bestaat het probleem nog steeds om te proberen de “gemiddelde” snelheid bij een bepaalde doorsnede weer te geven, aangezien in de vloeistofstroomvergelijkingen een gemiddelde waarde wordt gebruikt. Technisch gezien gebeurt dit door middel van integrale calculus. Praktisch, de student moet een gemiddelde waarde die de helft van de middellijn waarde te gebruiken.

viscositeit

viscositeit is een vloeistofeigenschap die de weerstand van de vloeistof tegen vervorming door een afschuifkracht meet., Viscositeit is de interne wrijving van een vloeistof waardoor het bestand is tegen stromen langs een vast oppervlak of andere lagen van de vloeistof. Viscositeit kan ook worden beschouwd als een maat voor de weerstand van een vloeistof tegen stroming. Een dikke olie heeft een hoge viscositeit; water heeft een lage viscositeit. De meeteenheid voor de absolute viscositeit is:

de viscositeit van een vloeistof is meestal sterk afhankelijk van de temperatuur van de vloeistof en relatief onafhankelijk van de druk., Voor de meeste vloeistoffen neemt de viscositeit van de vloeistof af naarmate de temperatuur van de vloeistof toeneemt. Een voorbeeld hiervan is de smeerolie van motoren. Wanneer de motor en de smeerolie koud zijn, is de olie erg viskeus of dik. Nadat de motor is gestart en de smeerolie in temperatuur toeneemt, neemt de viscositeit van de olie aanzienlijk af en lijkt de olie veel dunner.

ideale vloeistof

een ideale vloeistof is een vloeistof die niet drukkbaar is en geen viscositeit heeft., Ideale vloeistoffen bestaan eigenlijk niet, maar soms is het nuttig om te overwegen wat er zou gebeuren met een ideale vloeistof in een bepaalde vloeistofstroom probleem om het probleem te vereenvoudigen.

Reynolds-nummer

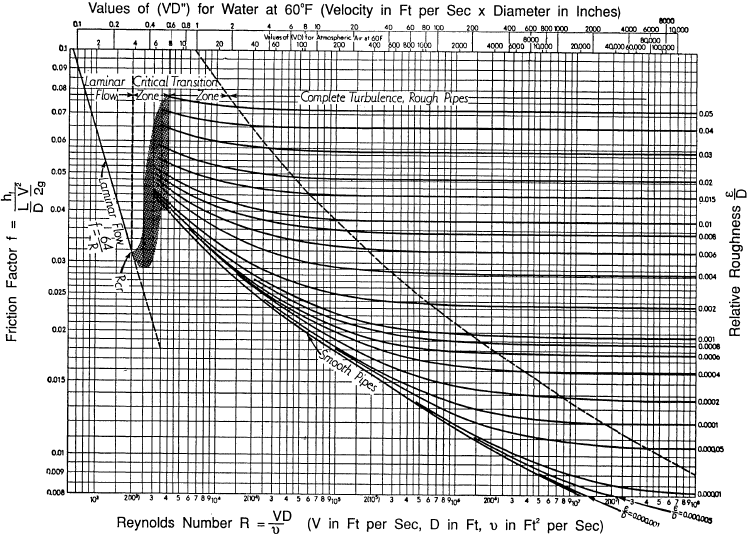
het stroomregime (laminair of turbulent) wordt bepaald door het Reynolds-nummer van de stroom te evalueren (zie Figuur 5). Het Reynolds-getal, gebaseerd op studies van Osborn Reynolds, is een dimensieloos getal dat bestaat uit de fysieke kenmerken van de stroom. Vergelijking 3-7 wordt gebruikt om het Reynolds-getal (NR) voor de vloeistofstroom te berekenen.,

waarbij:

voor praktische doeleinden, als het getal van Reynolds kleiner is dan 2000, is de stroom laminair. Als het groter is dan 3500, is de stroom turbulent. Stromen met Reynolds-nummers tussen 2000 en 3500 worden soms overgangsstromen genoemd. De meeste vloeistofsystemen in nucleaire installaties werken met turbulente stroming. Reynolds-getallen kunnen gemakkelijk worden bepaald met behulp van een Moody-grafiek, waarvan hieronder een voorbeeld wordt weergegeven. Nadere bijzonderheden over het gebruik van de Moody-Grafiek zijn te vinden in de volgende tekst.,