zeer informeel, de twee termen in de som gegeven door de Black-Scholes formule kunnen worden beschouwd als “de huidige prijs van het aandeel gewogen door de waarschijnlijkheid dat u uw optie om de voorraad te kopen zal uitoefenen “minus” de gereduceerde prijs van het uitoefenen van de optie gewogen door de waarschijnlijkheid dat u de optie zal uitoefenen”, of gewoon “wat u gaat krijgen “minus” wat u gaat betalen ” (Khan, 2013).,

voor een Europese putoptie (contracts for the right, but not obligation, to sell some underlaying asset at a pre-determined price on a pre-determined date in the future) is de equivalente functionele vorm:

voorbeeld: berekening van de prijs van een Europese calloptie

om te berekenen wat de prijs van een Europese calloptie zou moeten zijn, weten we dat we vijf waarden nodig hebben zoals vereist door vergelijking 6 hierboven. Zij zijn: 1. De huidige prijs van de voorraad (S), 2. De uitoefenprijs van de calloptie (X), 3. De tijd tot verval (T-t), 4. De risicovrije rentevoet (r) en 5., De volatiliteit van het bestand, gegeven door de standaardafwijking van historische logteruggaven (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

We kunnen de volatiliteit van elk aandeel schatten door de historische prijzen in acht te nemen, of, nog eenvoudiger, door andere optieprijzen voor hetzelfde aandeel op verschillende looptijden/vervaldatum (T) en uitoefen-/uitoefenprijzen (X) te berekenen, als we weten dat ze zijn vastgesteld volgens een Black-Scholes-model. De resulterende waarde, σ, is een getal tussen 0 en 1, die de impliciete volatiliteit van de markt voor het aandeel vertegenwoordigt., Voor Tesla bedroeg de gemiddelde waarde op het moment van schrijven van dit artikel ongeveer 0,38 voor 4-5 verschillende optieprijzen rond dezelfde vervaldatum/vervaldatum. Input in vergelijking 6 hierboven, vinden we dat de call optie die we geïnteresseerd zijn in zou moeten zijn prijzen ergens rond $7.

Impliciete Volatiliteit

hoewel het interessant is om te begrijpen hoe emittenten van opties tot de prijs van hun call-en putopties komen, is het voor beleggers moeilijk om per se met dergelijke prijzen “van mening te verschillen” en is het zo moeilijk om deze kennis om te zetten in bruikbare beleggingsthesissen.,

we kunnen echter veel milage uit de Black-Scholes formule halen als we in plaats daarvan de prijs van een optie (C of P) behandelen als een bekende hoeveelheid/onafhankelijke variabele (gevonden door te kijken naar verschillende looptijd/vervaldata T en verschillende uitoefenprijzen X). Dit omdat, als we dat doen, de Black-Scholes functional equation wordt een hulpmiddel om ons te helpen begrijpen hoe de markt schat de volatiliteit van een aandeel, ook bekend als de impliciete volatiliteit van de optie. Dit is informatie waar we het niet over eens kunnen zijn, en waar we tegen kunnen ruilen.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called “continuous timeline instruments”), they are much more difficult to deal with that European options (“point in time instruments”)., In de eerste plaats, omdat het optimale oefenbeleid de waarde van de optie zal beïnvloeden, moet hiermee rekening worden gehouden bij het oplossen van de Black-Scholes partiële differentiaalvergelijking. Er zijn geen bekende “gesloten vorm” oplossingen voor Amerikaanse opties volgens de Black-Scholes vergelijking. Er zijn echter enkele bijzondere gevallen:

• voor Amerikaanse callopties op onderliggende activa die geen dividend (of andere uitbetalingen) uitkeren, is de Amerikaanse calloptieprijs dezelfde als voor Europese callopties. Dit omdat het optimale oefeningsbeleid in dit geval is om de optie niet uit te oefenen.,
• voor Amerikaanse callopties op beleenbare activa die één bekend dividend uitkeren tijdens de looptijd ervan, kan het optimaal zijn om de optie vroegtijdig uit te oefenen., In dergelijke gevallen is de optie kan optimaal worden uitgeoefend net voordat de voorraad gaat ex-dividend, naar een oplossing gegeven in de gesloten vorm van de zogenaamde Roll-Geske-Whaley methode (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

ten Eerste, moet u controleren of het optimaal is voor de uitoefening van de optie vroeg, door te onderzoeken of de volgende ongelijkheid wordt voldaan:

voor s = aandelenkoers, X = uitoefenprijs, D₁ = uitbetaald dividend, t = huidige datum, t₁ = Datum van uitkering van dividend, T = vervaldatum van optie.

als de ongelijkheid niet wordt vervuld, is vroege oefening niet optimaal., Als C(・) is de regelmatige Black-Scholes formule voor het Europese call-opties op non-dividend-betalende voorraad eq (x), de waarde van de Amerikaanse call-optie wordt dan gegeven door een versie van dezelfde vergelijking waar de beurskoers (S) korting:

Als de ongelijkheid wordt voldaan, het begin van de oefening is optimaal en de waarde van de Amerikaanse call-optie wordt gegeven door de volgende, verschrikkelijk, puinhoop van een vergelijking (ik heb geprobeerd om het te breken door elke term, zodat ze beter leesbaar):

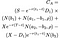
waarbij zoals voorheen S = koers van de aandelen, T = Datum van vervaldatum van de optie, X = uitoefenprijs en r= risicovrije rente, σ = volatiliteit (standaarddeviatie van het logboek van de historische rendementen van de aandelen), en D₁ de dividenduitkering is. Bovendien wordt ρ gegeven door:

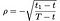
a₁, a₂ by:

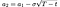
and b₁, b₂ by:

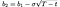
beperkingen

Het spreekt vanzelf dat het Black-Scholes-model precies dat is, een theoretisch model dat probeert te schatten hoe een markt zich gedraagt, gezien de bovenstaande aannames en de inherente beperkingen van onze eigen numerieke schattingen van risicovrije rentetarieven (r) en toekomstige volatiliteit (σ). Hier moet worden benadrukt dat niet alle veronderstellingen van (vooral het oorspronkelijke model) in feite empirisch geldig zijn., Bijvoorbeeld, aanzienlijke beperkingen ontstaan uit:

• De onderschatting van extreme bewegingen in de voorraad, waardoor staart risico
• De veronderstelling van instant -, kosten-minder handel, waardoor het liquiditeitsrisico
• De veronderstelling van een stationair proces, waardoor de volatiliteit
• De veronderstelling van constante en handel, opbrengst gap risk

Deze moeten worden opgenomen in alle strategieën, bijvoorbeeld door het afdekken met out-of-the-money opties, trading op meerdere beurzen, afdekking met volatiliteit van de afdekking en Gamma-afdekking, respectievelijk.,

Achtergrond

zoals kort vermeld waren het Fischer Black en Myron Scholes die in 1973 aantoonden dat een dynamische herziening van een portefeuille volgens bepaalde regels het verwachte rendement van het onderliggende effect wegneemt (Black & Scholes, 1973). Hun model bouwde voort op eerder gevestigde werken van Bachelier, Samuelson en anderen. Robert C. Merton was de eerste die een paper publiceerde over het begrip van het model en die de term “Black-Scholes options pricing model” bedacht., Scholes en Merton kregen in 1997 de Nobelprijs voor de Economische Wetenschappen voor hun ontdekking van de methode om aandelenopties te scheiden van het risico van hun onderliggende effecten. Toen Fischer Black in 1995 overleed, zou hij niet in aanmerking komen voor de prijs, maar werd erkend als bijdrager door de Nobel Academy.