gdy bezpłatny dodatni ładunek q jest przyspieszany przez pole elektryczne, otrzymuje energię kinetyczną (rysunek \(\pageindex{1}\))., Proces ten jest analogiczny do obiektu przyspieszanego przez pole grawitacyjne, tak jakby ładunek schodził w dół wzgórza elektrycznego, gdzie jego energia potencjalna elektryczna jest przekształcana w energię kinetyczną, chociaż oczywiście źródła sił są bardzo różne. Zbadajmy pracę wykonaną na ładunku q przez pole elektryczne w tym procesie, abyśmy mogli opracować definicję energii elektrycznej potencjalnej.

Siła elektrostatyczna lub Coulomba jest konserwatywna, co oznacza, że praca wykonywana na q jest niezależna od ścieżki, o czym później zademonstrujemy., Jest to dokładnie analogiczne do siły grawitacji. Gdy siła jest konserwatywna, można zdefiniować energię potencjalną związaną z siłą. Zwykle łatwiej jest pracować z energią potencjalną (ponieważ zależy to tylko od pozycji) niż obliczać pracę bezpośrednio.

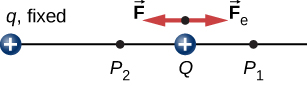
praca \(w_{12}\) wykonywana przez przyłożoną siłę \(\vec{F}\), gdy cząstka przesuwa się z \(P_1\) do \(p_2\) może być obliczona przez

\

gdzie zdefiniowaliśmy dodatnie, aby wskazywały odległość od źródła, A R jest odległością od źródła.pochodzenie. Kierunki zarówno przemieszczenia, jak i przyłożonej siły w układzie na rysunku \(\PageIndex{2}\) są równoległe, a zatem praca wykonana na układzie jest dodatnia.

używamy litery U do oznaczenia energii elektrycznej potencjalnej, która ma jednostki dżuli (J)., Gdy siła zachowawcza działa ujemnie, system zyskuje energię potencjalną. Gdy siła zachowawcza działa dodatnio, układ traci energię potencjalną, \(\Delta U = – w\). W układzie na rysunku \(\PageIndex{3}\) siła Coulomba działa w kierunku przeciwnym do przemieszczenia, dlatego praca jest ujemna. Zwiększyliśmy jednak energię potencjalną w układzie dwupłaszczowym.

w tym przykładzie praca W wykonywana w celu przyspieszenia dodatniego ładunku z odpoczynku jest dodatnia i wynika ze straty w U, lub ujemnej \(\Delta U\)., Wartość U można znaleźć w dowolnym punkcie, biorąc jeden punkt jako punkt odniesienia i obliczając pracę potrzebną do przeniesienia ładunku do drugiego punktu.

grawitacyjna energia potencjalna i elektryczna energia potencjalna są dość analogiczne. Energia potencjalna stanowi pracę wykonywaną przez konserwatywną siłę i daje dodatkowy wgląd w energię i transformację energii bez konieczności bezpośredniego czynienia z siłą. O wiele częściej, na przykład, używa się pojęcia energii elektrycznej potencjalnej niż do czynienia z siłą Coulomba bezpośrednio w rzeczywistych zastosowaniach.,

\

zauważ, że Q jest stałą.

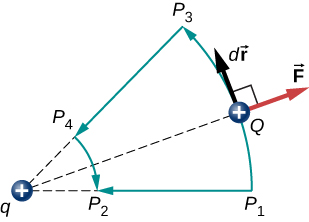
inną implikacją jest to, że możemy zdefiniować energię elektryczną potencjalną. Przypomnijmy, że praca wykonywana przez siłę zachowawczą wyraża się również jako różnica energii potencjalnej odpowiadającej tej sile., Dlatego praca \(w_{ref}\) sprowadzająca ładunek z punktu odniesienia do punktu zainteresowania może być zapisana jako

\

i, wzorem \ref{7.1}, różnica energii potencjalnej (\(U_2 – U_1\)) ładunku testowego Q pomiędzy dwoma punktami wynosi

\

dlatego możemy napisać ogólne wyrażenie dla energii potencjalnej dwóch ładunków punktowych (we współrzędnych sferycznych):

\_{r_{ref}}^r = KQQ\Left.,\]

możemy przyjąć drugi termin jako arbitralny stały poziom odniesienia, który służy jako zero odniesienia:

\

wygodnym wyborem odniesienia, który opiera się na naszym zdrowym rozsądku jest to, że gdy dwa ładunki są nieskończenie daleko od siebie, nie ma interakcji między nimi. (Przypomnijmy omówienie referencyjnej energii potencjalnej w energii potencjalnej i oszczędności energii.,) Przyjmując energię potencjalną tego stanu jako zero usuwa termin \(u_ {ref}\) z równania (tak jak wtedy, gdy mówimy, że ziemia jest zerową energią potencjalną w grawitacyjnym problemie energii potencjalnej), a energia potencjalna Q, gdy jest oddzielona od q przez odległość r przyjmuje postać

\

ze względu na prawo Coulomba, siły spowodowane wielokrotnymi ładunkami na ładunku testowym \(Q\) nakładają się; mogą być obliczane indywidualnie, a następnie dodawane. Oznacza to, że całki pracy i stąd wynikające z nich potencjalne Energie wykazują takie samo zachowanie., Aby to zademonstrować, rozważamy przykład montażu systemu czterech ładunków.

zauważ, że energia potencjalna elektryczna jest dodatnia, jeśli dwa ładunki są tego samego typu, dodatnie lub ujemne, i ujemne, jeśli dwa ładunki są przeciwnych typów. Ma to sens, jeśli pomyślisz o zmianie energii potencjalnej \(\Delta U\), gdy zbliżysz dwa ładunki lub przesuniesz je dalej od siebie., W zależności od względnych rodzajów opłat, być może będziesz musiał pracować nad systemem lub system zadziała na ciebie, to znaczy, że Twoja praca jest albo pozytywna, albo negatywna. Jeśli musisz wykonać pozytywną pracę nad systemem (faktycznie zbliżyć ładunki), energia systemu powinna wzrosnąć. Jeśli przyniesiesz dwa dodatnie lub dwa ujemne ładunki bliżej, musisz wykonać pozytywną pracę na systemie, która podnosi ich potencjalną energię. Ponieważ energia potencjalna jest proporcjonalna do 1 / r, energia potencjalna wzrasta, gdy r spada między dwoma dodatnimi lub dwoma ujemnymi ładunkami.,

z drugiej strony, jeśli zbliżysz ładunek dodatni i ujemny, musisz wykonać negatywną pracę na systemie( ładunki Cię ciągną), co oznacza, że odbierasz energię z systemu. Zmniejsza to energię potencjalną. Ponieważ energia potencjalna jest ujemna w przypadku dodatniej i ujemnej pary ładunków, wzrost o 1 / r sprawia, że energia potencjalna jest bardziej ujemna, co jest takie samo jak zmniejszenie energii potencjalnej.

wynik z przykładu \(\PageIndex{2}\) może zostać rozszerzony na systemy z dowolną liczbą opłat., W tym przypadku najwygodniej jest zapisać formułę jako

\

współczynnik 1/2 odpowiada za dwukrotne dodanie każdej pary opłat.