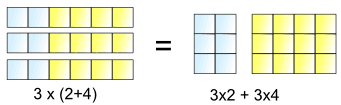Articles

Prawa komutacyjne, asocjacyjne i dystrybucyjne

by admin

Wow! Co za usta pełne słów! Ale pomysły są proste.

prawa przemienne

„prawa przemienne” mówią, że możemy zamienić się liczbami i nadal otrzymujemy tę samą odpowiedź …

… gdy dodamy:

a + b = b + a

przykład:

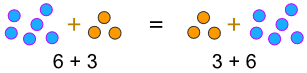
… lub gdy mnożymy:

a × b = b × a

przykład:

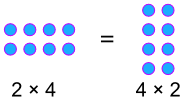
procenty przemienne!,

Ponieważ a × b = b × a prawdą jest również, że A% b = b% a

przykład: 8% z 50 = 50% z 8, czyli 4

Dlaczego „commutative”… ?

ponieważ liczby mogą podróżować tam iz powrotem jak dojeżdżający do pracy.

prawa asocjacyjne

„prawa asocjacyjne” mówią, że nie ma znaczenia, jak grupujemy liczby (tzn. które obliczamy jako pierwsze) …

…, kiedy dodajemy:

(A + b) + c = A + (b + c)

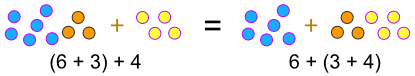
…,r>

This: (2 + 4) + 5 = 6 + 5 = 11 ma taką samą odpowiedź jak ta: 2 + (4 + 5) = 2 + 9 = 11

używa:

czasami łatwiej jest dodać lub pomnożyć w innej kolejności:

Co to jest 19 + 36 + 4?,

19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59

lub zmienić trochę:

Co to jest 2 × 16 × 5?

2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160

prawo dystrybucyjne

„prawo dystrybucyjne” jest najlepsze ze wszystkich, ale wymaga szczególnej uwagi.,

To jest to, co pozwala nam zrobić:

3 lots of (2+4) to to samo co 3 lots of 2 plus 3 lots of 4

tak więc 3× może być „rozłożone” na 2+4, na 3×2 i 3×4

i piszemy to tak:

a × (b + c) = a × b + a × c

wypróbuj obliczenia samodzielnie:

  • 3 × (2 + 4) = 3 × 6 = 18
  • 3×2 + 3×4 = 6 + 12 = 18

tak czy siak dostaje taką samą odpowiedź.,

po angielsku możemy powiedzieć:

otrzymujemy tę samą odpowiedź, gdy:

  • pomnożymy liczbę przez grupę liczb dodanych razem, lub
  • czy każdy mnożyć osobno, a następnie dodać je

używa:

czasami łatwiej jest rozbić trudne mnożenie:

przykład: co to jest 6 × 204 ?

6 × 204 = 6×200 + 6×4
= 1,200 + 24
= 1,224

lub połączyć:

przykład: co to jest 16 × 6 + 16 × 4?,

16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160

możemy użyć go również w odejmowaniu:

przykład: 26×3 – 24×3

26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6

przydałaby się też długa lista dodatków:

przykład: 6×7 + 2×7 + 3×7 + 5×7 + 4×7

6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140

. . . ale nie odchodź za daleko!,

prawo komutacyjne nie działa dla odejmowania lub dzielenia:

przykład:

  • 12/3 = 4, ale
  • 3/12 = ¼

prawo asocjacyjne nie działa dla odejmowania lub dzielenia:

Dodaj komentarz

Twój adres email nie zostanie opublikowany. Pola, których wypełnienie jest wymagane, są oznaczone symbolem *

This: (3 × 4) × 5 = 12 × 5 = 60
ma taką samą odpowiedź jak ta: 3 × (4 × 5) = 3 × 20 = 60