The Black-Scholes formula, explained (Polski)
bardzo nieformalnie, dwa terminy w sumie podane przez The Black-Scholes formula mogą być traktowane jako „aktualna cena akcji ważona przez prawdopodobieństwo, że będziesz korzystać z opcji zakupu akcji „minus” zdyskontowana Cena korzystania z opcji ważona przez prawdopodobieństwo, że będziesz korzystać z opcji”, lub po prostu „co masz zamiar dostać „minus” co masz zamiar zapłacić ” (Khan, 2013).,
w przypadku Europejskiej opcji sprzedaży (kontrakty na prawo, ale nie obowiązek, sprzedaży niektórych aktywów bazowych po wcześniej ustalonej cenie w określonym dniu w przyszłości) równoważna forma funkcjonalna to:


przykład: obliczanie ceny Europejskiej opcji kupna
aby obliczyć cenę Europejskiej opcji kupna, wiemy, że potrzebujemy pięciu wartości wymaganych przez równanie 6 powyżej. Są to: 1. Aktualna cena akcji (akcji), 2. Cena wykonania opcji call (X), 3. Czas do wygaśnięcia (T-t), 4. Stopa procentowa wolna od ryzyka (r) oraz 5., Zmienność akcji, określona przez odchylenie standardowe historycznych zwrotów logów (σ).
Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).
możemy oszacować zmienność akcji, obserwując ich historyczne ceny lub, jeszcze prościej, obliczając inne ceny opcji dla tych samych akcji w różnych terminach zapadalności/wygaśnięcia (T) i cenach wykonania / strajku (X), jeśli wiemy, że zostały ustalone zgodnie z modelem Black-Scholesa. Otrzymana wartość σ jest liczbą z zakresu od 0 do 1, reprezentującą implikowaną zmienność rynku dla akcji., W przypadku Tesli, w momencie pisania tego artykułu, wartość średnia wynosiła około 0,38 dla 4-5 różnych cen opcji w tym samym terminie wygaśnięcia / terminu zapadalności. Wejście do równania 6 powyżej, okazuje się, że opcja call jesteśmy zainteresowani powinny być ceny gdzieś około $7.
implikowana zmienność
chociaż interesujące jest zrozumienie, w jaki sposób emitenci opcji osiągają cenę opcji kupna i sprzedaży, jako inwestorzy trudno jest „nie zgodzić się” z takimi cenami, per se, i tak trudno przekształcić tę wiedzę w użyteczne tezy inwestycyjne.,
możemy jednak uzyskać wiele milage ze wzoru Black-Scholesa, jeśli zamiast tego potraktujemy cenę opcji (C lub P) jako znaną ilość / zmienną niezależną(znalezioną patrząc na różne terminy zapadalności / wygaśnięcia T i różne ceny ćwiczeń X). To dlatego, że jeśli to zrobimy, równanie funkcyjne Blacka-Scholesa stanie się narzędziem, które pomoże nam zrozumieć, w jaki sposób rynek szacuje zmienność akcji, znaną również jako implikowana zmienność opcji. To informacje, z którymi możemy się nie zgadzać, a z którymi handlować.,
Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.
American options
Because American options can be exercised at any date prior to expiration (so-called „continuous timeline instruments”), they are much more difficult to deal with that European options („point in time instruments”)., Przede wszystkim, ponieważ optymalna Polityka ćwiczeń wpłynie na wartość opcji, należy to wziąć pod uwagę przy rozwiązywaniu równania różniczkowego cząstkowego Blacka-Scholesa. Nie są znane rozwiązania” formy zamkniętej ” dla opcji amerykańskich według równania Blacka-Scholesa. Istnieją jednak pewne szczególne przypadki:
- w przypadku amerykańskich opcji call na aktywa bazowe, które nie wypłacają dywidendy (lub innych wypłat), Amerykańska cena opcji call jest taka sama jak w przypadku europejskich opcji call. To dlatego, że optymalna Polityka ćwiczeń w tym przypadku jest nie korzystać z opcji.,
- w przypadku amerykańskich opcji kupna na aktywa bazowe, które wypłacają jedną znaną dywidendę w ciągu swojego życia, optymalne może być wcześniejsze skorzystanie z opcji., W takich przypadkach opcja może być optymalnie wykorzystana tuż przed zwolnieniem akcji z dywidendy, zgodnie z rozwiązaniem podanym w formie zamkniętej metodą Roll-Geske-Whaleya (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):
najpierw sprawdź, czy optymalne jest wcześniejsze skorzystanie z opcji, badając, czy spełnione są następujące nierówności:

Dla S = Cena akcji, X = cena wykonania, D₁ = dywidenda wypłacona, t = data bieżąca, t₁ = Data wypłaty dywidendy, T = data wygaśnięcia opcji.
Jeśli nierówność nie jest spełniona, wczesne ćwiczenie jej nie jest optymalne., Jeśli C(・) jest regularną formułą Black-Scholesa dla europejskich opcji kupna na akcje niepłacące dywidendy (eq x), wartość amerykańskiej opcji kupna jest następnie podawana w wersji tego samego równania, w którym cena akcji jest dyskontowana:

div>
Jeśli nierówność jest spełniona, wczesne ćwiczenie jest optymalne, a wartość opcji American call jest podana przez następujący, okropny, bałagan równania (próbowałem podzielić je według każdego terminu, aby było bardziej czytelne):
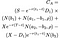
gdzie jak poprzednio S = Cena akcji, T = data wygaśnięcia opcji, X = cena wykonania i r = stopa procentowa wolna od ryzyka, σ = zmienność (odchylenie standardowe dziennika historycznych zysków akcji), a D₁ jest wypłatą dywidendy. Ponadto ρ jest podana przez:
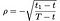
a₁, a₂ by:

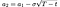
and b₁, b₂ by:

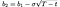
ograniczenia
nie trzeba dodawać, że model Black-Scholesa jest właśnie tym, modelem teoretycznym, który stara się oszacować zachowanie rynku, biorąc pod uwagę powyższe założenia i nieodłączne ograniczenia naszych własnych oszacowań numerycznych stóp procentowych wolnych od ryzyka (r) i przyszłej zmienności (σ). Należy w tym miejscu podkreślić, że nie wszystkie założenia (zwłaszcza oryginalnego modelu) są w rzeczywistości empirycznie poprawne., Na przykład, istotne ograniczenia wynikają z:
- niedoszacowania ekstremalnych ruchów na giełdzie, przynosząc ryzyko ogonowe
- założenia natychmiastowego, mniej kosztowego handlu, przynosząc ryzyko płynności
- założenia stacjonarnego procesu, przynosząc ryzyko zmienności
- założenia ciągłego czasu i handlu, przynosząc ryzyko luki
te powinny być uwzględniane we wszystkich strategiach inwestycyjnych, na przykład poprzez zabezpieczanie za pomocą out-of-the-money opcje, handel na wielu giełdach, hedging z zabezpieczeniem zmienności i gamma hedging, odpowiednio.,
Tło
jak krótko wspomniano, to Fischer Black i Myron Scholes w 1973 r.wykazali, że dynamiczna zmiana portfela zgodnie z pewnymi zasadami usuwa oczekiwany zwrot z bazowych zabezpieczeń (Black & Scholes, 1973). Ich model bazował na wcześniej ustalonych pracach Bacheliera, Samuelsona i innych. Robert C. Merton był pierwszym, który opublikował artykuł rozszerzający zrozumienie modelu i który ukuł termin „Black-Scholes options pricing model”., Scholes i Merton otrzymali w 1997 roku Nagrodę Nobla w dziedzinie nauk ekonomicznych za odkrycie metody oddzielania opcji na akcje od ryzyka związanego z ich bazowymi papierami wartościowymi. Po śmierci Fischera Blacka w 1995 r. nie mógł otrzymać nagrody, ale został uznany za współtwórcę przez Akademię Nobla.















