Når en gratis positive ladning q accelereres af et elektrisk felt, det er givet kinetisk energi (Figur \(\PageIndex{1}\))., Processen er analog med et objekt, der accelereres af et tyngdefelt, som om ladningen gik ned ad en elektrisk bakke, hvor dens elektriske potentielle energi omdannes til kinetisk energi, selvom kilderne til kræfterne naturligvis er meget forskellige. Lad os undersøge det arbejde, der udføres på en ladning q af det elektriske felt i denne proces, så vi kan udvikle en definition af elektrisk potentiel energi.

den elektrostatiske eller Coulomb kraft er konservativ, hvilket betyder, at arbejdet på q er uafhængigt af den sti, der er taget, som vi vil demonstrere senere., Dette er nøjagtigt analogt med tyngdekraften. Når en kraft er konservativ, er det muligt at definere en potentiel energi forbundet med kraften. Det er normalt lettere at arbejde med den potentielle energi (fordi det kun afhænger af position) end at beregne arbejdet direkte.

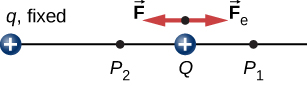
arbejdet \(W_{12}\) udført af den anvendte kraft \(\vec{F}\) når partiklen bevæger sig fra \(P_1\) til \(P_2\) kan beregnes ved at

\

\

hvor vi har defineret positivt at pege væk fra origo, og r er afstanden fra origo. Retningerne for både forskydningen og den påførte kraft i systemet i figur \(\Pageinde. {2}\) er parallelle, og dermed er arbejdet på systemet positivt.

Vi bruger bogstavet U til at betegne elektrisk potentiel energi, som har enheder af Joule (J)., Når en konservativ kraft gør negativt arbejde, får systemet potentiel energi. Når en konservativ kraft gør positivt arbejde, mister systemet potentiel energi, \(\Delta U= -\\). I systemet i figur \(\Pageinde. {3}\) virker Coulomb-kraften i modsat retning af forskydningen; derfor er arbejdet negativt. Vi har dog øget den potentielle energi i toladningssystemet.

i dette eksempel er arbejdet med at fremskynde en positiv ladning fra hvile positivt og skyldes et tab i U eller en negativ \(\Delta U\)., En værdi for U kan findes på ethvert tidspunkt ved at tage et punkt som reference og beregne det arbejde, der er nødvendigt for at flytte en afgift til det andet punkt.

gravitationspotentiale energi og elektrisk potentiel energi er ret analoge. Potentiel energi tegner sig for arbejde udført af en konservativ kraft og giver ekstra indsigt om energi og energitransformation uden nødvendigheden af at håndtere kraften direkte. Det er meget mere almindeligt, for eksempel at bruge begrebet elektrisk potentiel energi end at håndtere Coulomb-kraften direkte i virkelige applikationer.,

\

Bemærk, at Q er en konstant.

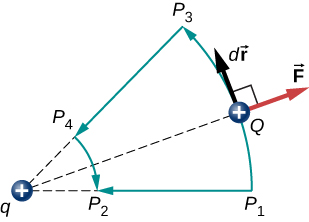
en anden implikation er, at vi kan definere en elektrisk potentiel energi. Husk, at det arbejde, der udføres af en konservativ kraft, også udtrykkes som forskellen i den potentielle energi, der svarer til den kraft., Derfor er det arbejde, \(W_{ref}\) for at bringe en ladning fra et referencepunkt til et punkt af interesse kan være skrevet som

\

og, ved Ligning, \ref{7.1}, forskellen i potentiel energi (\(U_2 – U_1\)) af test-afgift Q mellem de to punkter

\

Derfor, vi kan skrive et generelt udtryk for den potentielle energi af to punkt afgifter (i sfæriske koordinater):

\_{r_{ref}}^r = kqQ\venstre.,\]

Vi kan tage et andet udtryk for at være en vilkårlig konstant reference niveau, som fungerer som nul-reference:

\

Et passende valg af reference, der bygger på vores fælles fornemmelse er, at når de to afgifter er uendeligt langt fra hinanden, der er ingen interaktion mellem dem. (Husk diskussionen om referencepotentiel energi i potentiel energi og bevarelse af energi.,), Idet den potentielle energi af denne tilstand til at være nul fjerner udtrykket \(U_{ref}\) fra ligning (ligesom når vi siger, at jorden er nul potentielle energi i en gravitationel potentiel energi-problem), og den potentielle energi af Q, når det er adskilt fra q ved en afstand r antager form

\

på Grund af Coulomb ‘ s lov, den styrker på grund af flere debiteringer på et test afgift \Q\) oven; de kan beregnes individuelt og derefter tilføjet. Dette indebærer, at arbejdet integraler og dermed de resulterende potentielle energier udviser den samme adfærd., For at demonstrere dette overvejer vi et eksempel på at samle et system på fire ladninger.

Bemærk, at den elektriske potentielle energi er positiv, hvis de to afgifter er af samme type, enten positive eller negative, og negativ, hvis de to afgifter er de modsatte typer. Dette giver mening, hvis du tænker på ændringen i den potentielle energi \(\Delta U\), når du bringer de to ladninger nærmere eller flytter dem længere fra hinanden., Afhængigt af de relative typer afgifter skal du muligvis arbejde på systemet, eller systemet vil arbejde på dig, det vil sige, dit arbejde er enten positivt eller negativt. Hvis du skal gøre positivt arbejde på systemet (faktisk skubbe ladningerne tættere), skal systemets energi øges. Hvis du bringer to positive ladninger eller to negative ladninger tættere, skal du gøre positivt arbejde på systemet, hvilket øger deres potentielle energi. Da potentiel energi er proportional med 1 / r, går den potentielle energi op, når r går ned mellem to positive eller to negative ladninger.,

På den anden side, hvis du bringer en positiv og en negativ ladning nærmere, skal du gøre negativt arbejde på systemet (ladningerne trækker dig), hvilket betyder at du tager energi væk fra systemet. Dette reducerer den potentielle energi. Da potentiel energi er negativ i tilfælde af et positivt og et negativt ladningspar, gør stigningen i 1/r den potentielle energi mere negativ, hvilket er det samme som en reduktion i potentiel energi.

resultatet fra eksempel \(\Pageinde. {2}\) kan udvides til at omfatte systemer med et vilkårligt antal afgifter., I dette tilfælde er det bedst at skrive formlen som

\

faktoren på 1/2 konti for at tilføje hvert par afgifter to gange.