Meget uformelt, og de to begreber i summen givet af Black-Scholes formel kan opfattes som “den nuværende pris på aktien multipliceret med sandsynligheden for, at du vil udøve din mulighed for at købe aktien “minus” den nedsatte pris udnytte den mulighed, som er vægtet med sandsynligheden for, at du vil udnytte optionen’, eller blot ‘hvad du vil for at få “minus”, hvad du kommer til at betale ” (Khan, 2013).,

For en Europæisk put-option (kontrakter for retten, men ikke pligten, til at sælge nogle bagvedliggende aktiv til en på forhånd fastsat pris på et forud fastsat dato i fremtiden) den tilsvarende funktionelle form er:

Eksempel: Beregne prisen på en Europæisk call-option

for at beregne, hvad prisen på en Europæisk call-option bør være, vi ved, vi har brug for fem værdier, der kræves af ligning 6 ovenfor. De er: 1. Den aktuelle pris på bestanden (S), 2. Træningsprisen for call-optionen ()), 3. Tiden til udløb (T – T), 4. Den risikofrie rente (r) og 5., Volatiliteten i bestanden, givet ved standardafvigelsen af historiske log afkast (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

Vi kan estimere nogen materiel volatilitet ved at observere sin historiske priser, eller, endnu enklere, ved at beregne anden mulighed priser for den samme bestand på forskellige løbetider/udløbsdatoer (T) og motion/strejke priser (X), hvis vi ved, at de har været indstillet i henhold til en Black-Scholes-modellen. Den resulterende værdi, σ, er et tal mellem 0 og 1, der repræsenterer markedets implicitte volatilitet for bestanden., For Tesla, på tidspunktet for at skrive denne artikel, værdien i gennemsnit på ca 0,38 for 4-5 forskellige option priser omkring samme udløbsdato / forfaldsdato. Input i ligning 6 ovenfor finder vi, at den opkaldsmulighed, vi er interesseret i, skal være Priser et sted omkring $7.

underforstået volatilitet

selvom det er interessant at forstå, hvordan optionsudstedere ankommer til prisen på deres opkald og put-optioner, som investorer er det svært at “være uenig” med sådanne priser i sig selv og så svært at omdanne denne viden til handlingsrettede investeringsafhandlinger.,

Vi kan dog få en masse kilometer ud af Black-Scholes formlen, hvis vi i stedet behandle prisen på en option, C eller P) som en kendt mængde/uafhængige variable (fundet ved at kigge på forskellige løbetider/udløbsdatoer T og forskellige udnyttelseskurser X). Dette fordi, hvis vi gør det, Black-Scholes funktionelle ligning bliver et værktøj til at hjælpe os med at forstå, hvordan markedet estimerer volatiliteten af en bestand, også kendt som den implicitte volatilitet af optionen. Dette er oplysninger, vi kan være uenige om, og handel imod.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called “continuous timeline instruments”), they are much more difficult to deal with that European options (“point in time instruments”)., Primært, da den optimale øvelsespolitik vil påvirke værdien af optionen, skal dette tages i betragtning ved løsning af Black-Scholes partielle differentialligning. Der er ingen kendte “lukkede form” – løsninger til Amerikanske muligheder i henhold til Black-Scholes-ligningen. Der er dog nogle specielle tilfælde:

• for amerikanske opkaldsmuligheder på underliggende aktiver, der ikke betaler udbytte (eller andre udbetalinger), er den amerikanske opkaldspris den samme som for europæiske opkaldsmuligheder. Dette fordi den optimale træningspolitik i dette tilfælde er at ikke udøve muligheden.,
• for amerikanske call – optioner på underliggende aktiver, der betaler et kendt udbytte i sin levetid, kan det være optimalt at udøve muligheden tidligt., I sådanne tilfælde mulighed kan være optimalt udnyttet lige før materiel går ex-dividende, i henhold til en løsning, der er givet i lukket form af den såkaldte Roll-Geske-Whaley metode (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

kontroller Først, om det er optimalt at udnytte optionen tidligt, ved at undersøge, om følgende ulighed er opfyldt:

For S = aktiekurs, X = udnyttelseskurs, D₁ = betalt udbytte, t = aktuelle dato, t₁ = datoen for udbyttebetaling, T = udløbsdato mulighed.

Hvis uligheden ikke er opfyldt, tidlig motion det ikke optimalt., Hvis C(・) er den almindelige Black-Scholes formel for Europæiske call-optioner på ikke-dividende betalende lager (eq x), værdien af den Amerikanske call-option er givet ved en version af den samme ligning, hvor aktiekursen (S) er med rabat:

Hvis ulighed er opfyldt, tidligt motion er optimal, og værdien af den Amerikanske call-option er givet ved følgende, forfærdelig, rod i en ligning (jeg har forsøgt at bryde det op ved hver sigt at gøre det mere læsbart):

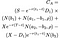
Hvor som før S = prisen på lager, T = tidspunkt for udløb af optionen, X = udnyttelseskursen og r = risikofrie rente, σ = volatiliteten (standardafvigelsen af log af det historiske afkast på aktiemarkedet), og D₁ er den dividende udbetaling. Hertil kommer, ρ, er givet ved:

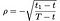
a₁, a₂ by:

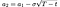
and b₁, b₂ by:

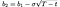
Begrænsninger

Det bør gå uden at sige, at Black-Scholes modellen er netop, at en teoretisk model, der forsøger at vurdere, hvordan markedet opfører sig, givet de antagelser, der er anført ovenfor, og de begrænsninger, som vores egen numeriske beregninger af risiko-fri rente (r) og fremtidige volatilitet (σ). Det skal her fremhæves, at ikke alle antagelser om (især den oprindelige model) faktisk er empirisk gyldige., For eksempel, betydelige begrænsninger opstår fra:

• undervurdering af ekstreme bevægelser i aktiemarkedet, giver hale risiko
• Den antagelse, instant, cost-mindre handel, giver likviditetsrisiko
• antagelse af en stationær proces, rente volatilitet risiko
• en antagelse om kontinuerlig tid og handel, giver afstanden risiko

Disse skal behandles i alle investeringsstrategier, for eksempel ved afdækning med out-of-the-money optioner, handel på flere børser, afdækning med volatilitet afdækning og Gamma afdækning, hhv.,

Baggrund

Som kort nævnt, at det var Fischer Black og Myron Scholes, der i 1973 viste, at dynamisk revidere en portefølje i henhold til bestemte regler fjerner det forventede afkast på det underliggende værdipapir (Sort & Scholes, 1973). Deres model bygget på tidligere etablerede værker af Bachelier, Samuelson og andre. Robert C. Merton var den første til at offentliggøre et papir, der udvidede forståelsen af modellen, og som opfandt udtrykket “Black-Scholes options pricing model”., Scholes og Merton blev tildelt nobelprisprisen i økonomi i 1997 for deres opdagelse af metoden til at skille aktieoptioner fra risikoen for deres underliggende værdipapirer. Da Fischer Black døde i 1995, ville han ikke være berettiget til at modtage prisen, men blev anerkendt som bidragyder af Nobel Academy.