Tilbage til Lektioner Index | Gøre Erfaringer med Henblik | Print-venlig side

Den Rationelle Rødder Test: Introduktion (side 1 af 2)

nul af et polynomium er en input-værdi (normalt en x-værdi), som returnerer en værdi på nul for hele polynomium, når du sætter det ind i polynomiet. Når et nul er et reelt (det vil sige ikke komplekst) tal, er det også en pol-aflytning af grafen for polynomfunktionen., Du vil ofte (især i calculus) ønsker at vide placeringen af nuller af en given polynomiel funktion. Du kan sætte tal ind i polynomiet, vilje, og håber på det bedste. Men som du lærte, da du studerede den kvadratiske formel, nuller er ofte meget rodet tal; tilfældigt gætte er nok ikke den bedste plan for angreb. Så hvordan går man om at forsøge at finde nuller?

den rationelle rødder (eller rationelle nuller) Test er en praktisk måde at opnå en liste over nyttige første gæt, når du forsøger at finde nuller (rødder) af et polynomium., I betragtning af et polynomium med heltal (det vil sige positive og negative “hele tal”) koefficienter, findes de mulige (eller potentielle) nuller ved at notere faktorerne for den konstante (sidste) periode over faktorerne for den førende koefficient og danner således en liste over fraktioner. Denne liste giver dig en liste over potentielle rationelle (brøkdele) rødder til at teste-deraf navnet på testen.

Lad mig understrege: den rationelle Roots Test giver dig ikke nullerne. Det siger ikke, hvad nullerne helt sikkert vil være., Testen giver dig kun en liste over relativt lette og” pæne ” numre at prøve i polynomet. De fleste af disse mulige nuller vil vise sig faktisk ikke at være nuller!

Du kan se følelsen af testens metode ved at se på et simpelt polynom. I betragtning af den kvadratiske 12×2 – 7x – 10, kan du bruge den Kvadratiske Formlen til at finde de nuller, men du kan også faktor for at få 12×2 – 7x – 10 = (3x + 2)(4x – 5). Indstilling af to faktorer lig med nul, får du to rødder på = = – 2/3 og 5 = 5/4., Bemærk, at betegnelserne “3” og “4” er faktorer af den førende koefficient “12”, og tællerne “2” og “5”er faktorer af det konstante udtryk “10”. Det vil sige, at nullerne er fraktioner dannet af faktorer af det konstante udtryk (10) over faktorer af den førende koefficient (12). Bemærk dog også, at fraktioner som 5/6 og-10/3 også kan dannes på denne måde (og dermed leveres til dig ved testen), men disse andre fraktioner er faktisk ikke nuller af denne kvadratiske.,

dette forhold er altid sandt: hvis et polynom har rationelle rødder, vil disse rødder være fraktioner af formen (plus-eller-minus) (faktor for det konstante udtryk) / (faktor for den førende koefficient). Imidlertid er ikke alle fraktioner af denne form nødvendigvis nuller af polynomet. Faktisk kan det ske, at ingen af de således dannede fraktioner faktisk er et nul af polynomet.

Bemærk, at jeg fortsat siger “potentielle” rødder, “mulige” nuller”, hvis der er sådanne rødder…”., Dette skyldes, at listen over fraktioner genereret af Rational Roots-testen kun er en liste over potentielle løsninger. Det behøver ikke være sandt, at nogen af fraktionerne faktisk er en løsning. Der kan ikke være nogen brøkdele rødder! For eksempel, da x2 – 2, den Rationelle Rødder Tests giver følgende mulige rationelle nuller:

Men du ved allerede, at:

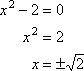
…så nuller er faktisk ikke rationelt overhovedet.,

husk altid: testen Rational Roots giver kun en liste over gode første gæt; det giver dig ikke “svarene”!

• Find alle mulige rationelle intercep-aflytninger af44 + 2 .3 – 7 .2 – 8. + 12.

Top | 1 | 2 | Return to Index Next >>