Articles

Kommutative, Associative og Distributive Love

by admin

Wowo!! Hvilken mundfuld af ord! Men ideerne er enkle.

kommutative Love

“kommutative love” siger, at vi kan bytte tal over og stadig få det samme svar …

… når vi tilføjer:

a + b = b + a

eksempel:

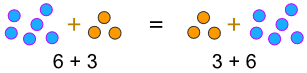
… eller når vi multiplicerer:

a b b = b!a

eksempel:

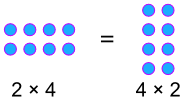
kommutative procentdele!,

Fordi a × b = b × a det er også sandt, at en% af b = b% af en

Eksempel: 8% af 50 = 50% 8, der er 4

Hvorfor “kommutativ” … ?

fordi tallene kan rejse frem og tilbage som en pendler.

Associative Love

“Associative Love” sige, at det ikke er ligegyldigt, hvordan vi gruppe numre (dvs som vi beregner først) …

…, da vi tilføje:

(a + b) + c = a + (b + c)

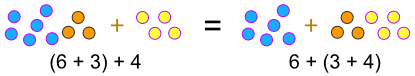
…,r>

Her: (2 + 4) + 5 = 6 + 5 = 11 Har de samme svar som dette: 2 + (4 + 5) = 2 + 9 = 11

Her: (3 × 4) × 5 = 12 × 5 = 60
Har de samme svar som dette: 3 × (4 × 5) = 3 × 20 = 60

Bruger:

nogle gange er det nemmere at tilføje eller formere sig i en anden rækkefølge:

Hvad er 19 + 36 + 4?,

19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59

Eller for at flytte om lidt:

Hvad er 2 × 16 × 5?

2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160

Distributive Lov

“Distributive Lov” er den BEDSTE af alle, men kræver omhyggelig opmærksomhed.,

Dette er, hvad det lader os gøre:

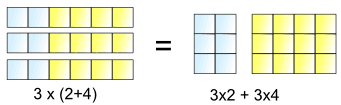
3. masser af (2+4) er det samme som 3 masser af 2 plus 3 masser af 4

Så, den 3× kan være “fordelt” på tværs af de 2+4, i 3×2 og 3×4

Og vi skrive det lide dette:

a × (b + c) = a × b + a × c

Prøv beregningerne dig selv:

  • 3 × (2 + 4) = 3 × 6 = 18
  • 3×2 + 3×4 = 6 + 12 = 18

Enten måde får det samme svar.,

I dansk kan vi sige:

Vi få det samme svar, når vi:

  • ganger et tal med en gruppe af numre, der er føjet sammen, eller
  • gør hver formere sig separat, så tilføj dem

Bruger:

nogle gange er det er lettere at bryde op en vanskelig multiplikation:

Eksempel: Hvad er 6 × 204 ?

6 × 204 = 6×200 + 6×4
= 1,200 + 24
= 1,224

Eller for at kombinere:

Eksempel: Hvad er 16 × 6 + 16 × 4?,

16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160

Vi kan bruge det i subtraktion for:

Eksempel: 26×3 – 24×3

26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6

Vi kan bruge det til en lang liste af tilføjelser, for:

Eksempel: 6×7 + 2×7 + 3×7 + 5×7 + 4×7

6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 x 7
= 140

. . . men gå ikke for langt!,

Den Kommutative Lov virker ikke for subtraktion eller division:

Eksempel:

  • 12 / 3 = 4, men
  • 3 / 12 = ¼

Den Associative Lov virker ikke for subtraktion eller division: