es acelerado por un campo eléctrico, se le da energía cinética (figura \(\pageIndex{1}\))., El proceso es análogo a un objeto que es acelerado por un campo gravitacional, como si la carga descendiera por una colina eléctrica donde su energía potencial eléctrica se convierte en energía cinética, aunque por supuesto las fuentes de las fuerzas son muy diferentes. Exploremos el trabajo realizado en una carga q por el campo eléctrico en este proceso, para que podamos desarrollar una definición de energía potencial eléctrica.

la fuerza electrostática o de Coulomb es conservadora, lo que significa que el trabajo realizado en q es independiente del camino tomado, como demostraremos más adelante., Esto es exactamente análogo a la fuerza gravitacional. Cuando una fuerza es conservadora, es posible definir una energía potencial asociada con la fuerza. Por lo general, es más fácil trabajar con la energía potencial (porque depende solo de la posición) que calcular el trabajo directamente.

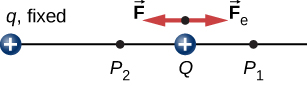
El trabajo \(W_{12}\) realizado por la fuerza aplicada \(\vec{F}\) cuando la partícula se mueve desde \(P_1\) a \(P_2\) puede ser calculado

\

\

donde hemos definido positivo que se apunta lejos del origen y r es la distancia desde el origen. Las direcciones tanto del desplazamiento como de la fuerza aplicada en el sistema en la figura \(\PageIndex{2}\) son paralelas, y por lo tanto el trabajo realizado en el sistema es positivo.

usamos la letra U para denotar energía potencial eléctrica, que tiene unidades de julios (J)., Cuando una fuerza conservadora hace un trabajo negativo, el sistema gana energía potencial. Cuando una fuerza conservadora hace un trabajo positivo, el sistema pierde energía potencial, \(\Delta U = – W\). En el sistema de la figura \(\PageIndex{3}\), la fuerza de Coulomb actúa en la dirección opuesta al desplazamiento; por lo tanto, el trabajo es negativo. Sin embargo, hemos aumentado la energía potencial en el sistema de dos cargas.

en este ejemplo, el trabajo W realizado para acelerar una carga positiva del reposo es positivo y resulta de una pérdida en U, o un \negativo(\Delta U\)., Un valor para U se puede encontrar en cualquier punto tomando un punto como referencia y calculando el trabajo necesario para mover una carga al otro punto.

La energía potencial gravitacional y la energía potencial eléctrica son bastante análogas. La energía potencial representa el trabajo realizado por una fuerza conservadora y da una visión adicional sobre la energía y la transformación de la energía sin la necesidad de tratar con la fuerza directamente. Es mucho más común, por ejemplo, utilizar el concepto de energía potencial eléctrica que tratar con la fuerza de Coulomb directamente en aplicaciones del mundo real.,

\

tenga en cuenta que P es una constante.

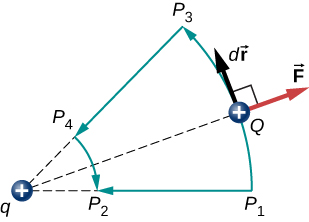
Otra implicación es que podemos definir una energía potencial eléctrica. Recordemos que el trabajo realizado por una fuerza conservadora también se expresa como la diferencia en la energía potencial correspondiente a esa fuerza., Por lo tanto, el trabajo \(w_{ref}\) para llevar una carga desde un punto de referencia a un punto de interés puede escribirse como

\

y, por ecuación \ref{7.1}, la diferencia en energía potencial (\(U_2 – U_1\)) de la carga de prueba Q entre los dos puntos es

\

por lo tanto, podemos escribir una expresión general para la energía potencial de dos cargas puntuales (en coordenadas esféricas):

\_{R_{ref}}^R = kqq\left.,\]

podemos tomar el segundo término como un nivel de referencia constante arbitrario, que sirve como la referencia cero:

\

una opción conveniente de referencia que se basa en nuestro sentido común es que cuando las dos cargas están infinitamente separadas, no hay interacción entre ellas. (Recordemos la discusión de la energía potencial de referencia en energía potencial y conservación de energía., Tomando la energía potencial de este estado como cero elimina el término \(u_{ref}\) de la ecuación (al igual que cuando decimos que el suelo es energía potencial cero en un problema de energía potencial gravitacional), y la energía potencial de Q cuando se separa de q por una distancia r asume la forma

\

debido a la Ley de Coulomb, las fuerzas debido a múltiples cargas en una carga de prueba \(Q\) se superponen; pueden calcularse individualmente y luego agregarse. Esto implica que las integrales de trabajo y por lo tanto las energías potenciales resultantes exhiben el mismo comportamiento., Para demostrar esto, consideramos un ejemplo de montaje de un sistema de cuatro cargas.

tenga en cuenta que la energía potencial eléctrica es positiva si las dos cargas son del mismo tipo, ya sea positiva o negativa, y negativa si las dos cargas son de tipos opuestos. Esto tiene sentido si piensa en el cambio en la energía potencial \(\Delta U\) a medida que Acerca las dos cargas o las aleja más., Dependiendo de los tipos relativos de cargos, Es posible que tenga que trabajar en el sistema o el sistema funcionaría en usted, es decir, su trabajo es positivo o negativo. Si usted tiene que hacer un trabajo positivo en el sistema (en realidad empujar las cargas más cerca), entonces la energía del sistema debe aumentar. Si acercas dos cargas positivas o dos cargas negativas, tienes que hacer un trabajo positivo en el sistema, lo que aumenta su energía potencial. Dado que la energía potencial es proporcional a 1 / r, la energía potencial sube cuando r baja entre dos cargas positivas o dos negativas.,

por otro lado, si acercas una carga positiva y una negativa, tienes que hacer un trabajo negativo en el sistema (las cargas te están tirando), lo que significa que quitas energía del sistema. Esto reduce la energía potencial. Dado que la energía potencial es negativa en el caso de un par de carga positiva y negativa, el aumento en 1/r hace que la energía potencial sea más negativa, lo que es lo mismo que una reducción en la energía potencial.

el resultado del ejemplo \(\PageIndex{2}\) puede extenderse a sistemas con cualquier número arbitrario de cargas., En este caso, es más conveniente escribir la fórmula como

\

el factor de 1/2 cuenta para agregar cada par de cargos dos veces.