muy informalmente, los dos términos en la suma dada por la fórmula de Black-Scholes pueden ser pensados como ‘el precio actual de la acción ponderado por la probabilidad de que ejercites tu opción de comprar la acción’ menos ‘el precio descontado de ejercer la opción ponderado por la probabilidad de que ejercites la opción’, o simplemente ‘lo que vas a obtener’ menos ‘lo que vas a pagar’ (Khan, 2013).,

Para una opción put Europea (contratos para el derecho, pero no la obligación, a vender parte inferior activo a un precio determinado en una determinada fecha en el futuro), el equivalente a la forma funcional es:

ejemplo: calcular el precio de una opción de compra Europea

para calcular cuál debe ser el precio de una opción de compra Europea, sabemos que necesitamos cinco valores requeridos por la ecuación 6 anterior. Son: 1. El precio actual de las acciones, 2. El precio de ejercicio de la opción de compra (X), 3. El tiempo hasta la expiración (T – t), 4. El tipo de interés Libre de riesgo (r) y 5., La volatilidad de la acción, dada por la desviación estándar del registro histórico devuelve (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

podemos estimar la volatilidad de cualquier acción observando sus precios históricos, o, aún más simple, calculando otros precios de opción para la misma acción en diferentes fechas de vencimiento / vencimiento (T) y precios de ejercicio/ejercicio (X), si sabemos que se han establecido de acuerdo con un modelo de Black-Scholes. El valor resultante, σ, es un número entre 0 y 1, que representa la volatilidad implícita del mercado para la acción., Para Tesla, en el momento de escribir este artículo, el valor promedio era de Aproximadamente 0.38 para 4-5 precios de opciones diferentes alrededor de la misma fecha de vencimiento/vencimiento. Entrada en la ecuación 6 anterior, encontramos que la opción de llamada que estamos interesados en DEBE SER precios en algún lugar alrededor de $7.

volatilidad implícita

aunque es interesante entender cómo los emisores de opciones llegan al precio de sus opciones de compra y venta, como inversores es difícil «estar en desacuerdo» con tales precios, per se, y tan difícil convertir este conocimiento en tesis de inversión accionables.,

sin embargo, podemos obtener una gran cantidad de milage de la fórmula de Black-Scholes si en su lugar tratamos el precio de una opción (C O P) como una cantidad conocida/variable independiente (que se encuentra mirando diferentes fechas de vencimiento/vencimiento T y diferentes precios de ejercicio X). Esto porque, si lo hacemos, la ecuación funcional de Black-Scholes se convierte en una herramienta para ayudarnos a entender cómo el mercado estima la volatilidad de una acción, también conocida como la volatilidad implícita de la opción. Esta es información sobre la que podemos estar en desacuerdo y contra la que podemos negociar.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called «continuous timeline instruments”), they are much more difficult to deal with that European options («point in time instruments”)., Principalmente, dado que la política de ejercicio óptimo afectará el valor de la opción, esto debe tenerse en cuenta al resolver la ecuación diferencial parcial de Black-Scholes. No hay soluciones conocidas de «forma cerrada» para las opciones estadounidenses de acuerdo con la ecuación de Black-Scholes. Sin embargo, hay algunos casos especiales:

• para las opciones de compra estadounidenses sobre activos subyacentes que no pagan dividendos (u otros pagos), el precio de la opción de compra estadounidense es el mismo que para las opciones de compra europeas. Esto porque la política óptima de ejercicio en este caso es no ejercer la opción.,
• para las opciones de compra estadounidenses sobre activos subyacentes que pagan un dividendo conocido en su vida útil, puede ser óptimo ejercer la opción antes., En tales casos, la opción puede ejercerse de manera óptima justo antes de que la acción pase ex dividendo, de acuerdo con una solución dada en forma cerrada por el llamado método Roll-Geske-Whaley (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

primero, verifique si es óptimo ejercer la opción temprano, investigando si se cumple la siguiente desigualdad:

para S = precio de acciones, X = Precio de ejercicio, D = = dividendo pagado, t = fecha actual, t = = fecha de pago del dividendo, T = fecha de vencimiento de la opción.

si la desigualdad no se cumple, el ejercicio temprano no es óptimo., Si C(・) es la fórmula regular de Black-Scholes para las opciones de compra europeas sobre acciones que no pagan dividendos (eq x), el valor de la opción de compra estadounidense se da por una versión de la misma ecuación donde se descuenta el precio de las acciones:

Si la desigualdad se cumple, a principios de ejercicio es óptimo y el valor de la opción call Americana está dado por la siguiente, horrible, un lío de una ecuación (traté de romper por cada término para hacerlo más legible):

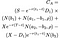
donde como antes S = precio de la acción, T = fecha de vencimiento de la opción, X = Precio de ejercicio y R = tasa de interés Libre de riesgo, σ = volatilidad (desviación estándar del registro de los rendimientos históricos de la acción), y D is es el pago de dividendos. Además, ρ es dada por:

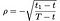
a₁, a₂ by:

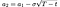
and b₁, b₂ by:

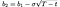
limitaciones

no hace falta decir que el modelo de Black-Scholes es precisamente eso, un modelo teórico que trata de estimar cómo se comporta un mercado, dadas las suposiciones expuestas anteriormente y las limitaciones inherentes de nuestras propias estimaciones numéricas de tasas de interés libres de riesgo (r) y volatilidad futura (σ). Cabe destacar aquí que no todos los supuestos de (especialmente el modelo original) son de hecho empíricamente válidos., Por ejemplo, las limitaciones significativas surgen de:

• la subestimación de movimientos extremos en la acción, rindiendo riesgo de cola
• La suposición de operaciones instantáneas, sin costos, rindiendo riesgo de liquidez
• La suposición de un proceso estacionario, rindiendo riesgo de volatilidad
• La suposición de tiempo continuo y negociación, rindiendo riesgo de brecha

estos deben tenerse en cuenta en todas y cada una de las estrategias de inversión, por ejemplo, múltiples intercambios, cobertura con cobertura de volatilidad y cobertura gamma, respectivamente.,

Background

como se mencionó brevemente, fueron Fischer Black y Myron Scholes quienes en 1973 mostraron que la revisión dinámica de una cartera de acuerdo con ciertas reglas elimina el retorno esperado de la seguridad subyacente (Black & Scholes, 1973). Su modelo se basa en obras previamente establecidas por Bachelier, Samuelson y otros. Robert C. Merton fue el PRIMERO en publicar un artículo expandiendo la comprensión del modelo y quien acuñó el término «Black-Scholes options pricing model»., Scholes y Merton fueron galardonados con el Premio Nobel en 1997 en Ciencias Económicas por su descubrimiento del método de divorciar las opciones de acciones del riesgo de sus valores subyacentes. Como Fischer Black falleció en 1995, no sería elegible para recibir el premio, pero fue reconocido como colaborador por la Academia Nobel.