El Cero de un polinomio es una entrada valor (generalmente un valor X) que devuelve un valor de cero para todo el polinomio cuando lo enchufas en el polinomio. Cuando un cero es un número real (es decir, no complejo), también es una intersección x del gráfico de la función polinómica., Con frecuencia (especialmente en cálculo) querrá saber la ubicación de los ceros de una función polinómica dada. Usted podría conectar números en el polinomio, willy-nilly, y esperar lo mejor. Pero como aprendiste cuando estudiaste la fórmula cuadrática, los ceros a menudo son números muy desordenados; adivinar al azar probablemente no sea el mejor plan de ataque. Entonces, ¿cómo se trata de encontrar ceros?

la prueba de raíces racionales (o ceros racionales) es una forma práctica de obtener una lista de primeras conjeturas útiles cuando está tratando de encontrar los ceros (raíces) de un polinomio., Dado un polinomio con coeficientes enteros (es decir, positivos y negativos), los ceros posibles (o potenciales) se encuentran enumerando los factores de la constante (último) término sobre los factores del coeficiente principal, formando así una lista de fracciones. Esta lista le da una lista de raíces racionales potenciales (fraccionales) para probar hence de ahí el nombre de la prueba.

permítanme enfatizar: la prueba de raíces racionales no le da los ceros. No dice lo que los ceros definitivamente., La prueba solo le da una lista de números relativamente fáciles y «agradables» para probar en el polinomio. ¡La mayoría de estos ceros posibles resultarán no ser realmente ceros!

puede ver el sentido de la metodología de la prueba mirando un polinomio simple. Dado el cuadrático 12×2-7x – 10, puede usar la fórmula cuadrática para encontrar los ceros, pero también puede factorizar para obtener 12×2 – 7x – 10 = (3x + 2)(4x-5). Estableciendo los dos factores iguales a cero, obtienes dos raíces en x = – 2/3 y x = 5/4., Tenga en cuenta que los denominadores «3» y «4» son factores del coeficiente principal «12», y los numeradores «2» y «5» son factores del término constante «10». Es decir, los ceros son fracciones formadas por factores del término constante (10) sobre Factores del coeficiente principal (12). Tenga en cuenta también, sin embargo, que las fracciones tales como 5/6 y – 10/3 también se pueden formar de esta manera (y por lo tanto ser proporcionado a usted por la prueba), pero estas otras fracciones no son de hecho ceros de esta cuadrática.,

esta relación es siempre verdadera: si un polinomio tiene raíces racionales, entonces esas raíces serán fracciones de la forma (más o menos) (factor del término constante) / (factor del coeficiente principal). Sin embargo, no todas las fracciones de esta forma son necesariamente ceros del polinomio. De hecho, puede suceder que ninguna de las fracciones así formadas es en realidad un cero del polinomio.

tenga en cuenta que sigo diciendo raíces «potenciales», «posibles» ceros», si hay tales raíces…»., Esto se debe a que la lista de fracciones generadas por la prueba de raíces racionales es solo una lista de soluciones potenciales. No tiene por qué ser cierto que cualquiera de las fracciones es en realidad una solución. ¡Puede que no haya raíces fraccionarias! Por ejemplo, dada x2 – 2, la Racional Raíces Pruebas da las siguientes posibles ceros racionales:

Pero usted ya sabe que:

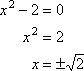
…así que los ceros no son en realidad racionales a todos los.,

siempre recuerde: la prueba de raíces racionales solo da una lista de buenas primeras conjeturas; ¡ no le da «las» respuestas!

• Encuentra todas las posibles intercepciones racionales x De x4 + 2×3-7×2-8x + 12.

Top | 1 | 2 | Return to Index Next >>