Kun ilmainen positiivinen varaus q kiihdytetään sähkökentässä, se on annettu liike-energia (Luku \(\PageIndex{1}\))., Prosessi on samanlainen esine on nopeutettu, jonka painovoimakenttä, kuin jos maksu oli menossa alas sähköinen hill, jossa sen sähköinen potentiaalienergia muuttuu liike-energiaa, vaikka tietenkin lähteet voimat ovat hyvin erilaisia. Olkaamme tutkia työstä maksu q sähkökenttä tässä prosessissa, jotta voimme kehittää määritelmä sähköinen potentiaalienergia.

sähköstaattinen tai Coulombin voima on konservatiivinen, mikä tarkoittaa, että työstä q on riippumaton polun otettu, kun me osoitamme myöhemmin., Tämä vastaa gravitaatiovoimaa. Kun voima on konservatiivinen, on mahdollista määritellä voimaan liittyvä potentiaalienergia. Se on yleensä helpompi työskennellä potentiaalienergia (koska se riippuu vain kanta) kuin laskea toimi suoraan.

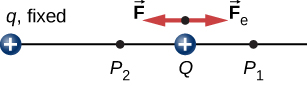
työ \(W_{12}\) tehty kohdistettu voima \(\vec{F}\), kun hiukkanen siirtyy \(P_1\) on \(P_2\) voidaan laskea

\

\

missä olemme määritelleet positiivisen osoittaa pois origosta ja r on etäisyys origosta. Kuvassa \(\PageIndex{2}\) sekä järjestelmän siirtymän että sovelletun voiman suunnat ovat samansuuntaisia, ja näin ollen järjestelmällä tehty työ on positiivista.

käytämme kirjainta U kuvaamaan sähköistä potentiaalienergiaa, jossa on joules (J) – yksiköitä., Kun konservatiivinen voima tekee negatiivista työtä, järjestelmä saa potentiaalista energiaa. Kun konservatiivinen voima tekee positiivista työtä, järjestelmä menettää potentiaalienergian, \(\Delta U = – W\). Järjestelmässä Luku \(\PageIndex{3}\), Coulombin voima toimii vastakkaiseen suuntaan siirtymä; siksi työ on negatiivinen. Olemme kuitenkin lisänneet kahden latauksen järjestelmän potentiaalista energiaa.

tässä esimerkki, työ W tehnyt nopeuttaa positiivinen varaus muualta on positiivinen ja tuloksia tappio U, tai negatiivinen \(\Delta U\)., U: n arvo löytyy mistä tahansa pisteestä ottamalla vertailukohdaksi yhden pisteen ja laskemalla työn, joka tarvitaan latauksen siirtämiseksi toiseen pisteeseen.

Gravitaatiopotentiaalienergia ja sähköinen potentiaalienergia ovat melko analogisia. Mahdollisia energian osuus työstä on konservatiivinen voima, ja antaa lisää tietoa koskien energiaa ja energian muuntaminen ilman tarvetta käsittelevät voima suoraan. Esimerkiksi sähkökäyttöisen potentiaalienergian käsitteen käyttö on paljon yleisempää kuin Coulombin voiman käsitteleminen suoraan reaalimaailman sovelluksissa.,

\

Huomaa, että Q on vakio.

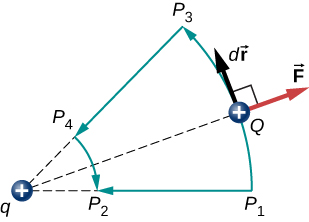
toinen vihjaus on, että saatamme määritellä sähköistä potentiaalienergiaa. Muistuttaa, että konservatiivisen voiman tekemä työ ilmaistaan myös kyseistä voimaa vastaavan potentiaalienergian erona., Siksi työ \(W_{ref}\) tuoda veloituksetta lähtökohtana kiinnostava voi olla kirjallinen kuten

\

ja, Yhtälön \ref{7.1}, erotus potentiaalista energiaa (\(U_2 – U_1\)) testin varaus Q välillä on kaksi pistettä.

\

näin Ollen, voimme kirjoittaa yleinen lauseke potentiaalienergia kahden pisteen maksut (pallomainen koordinaatit):

\_{r_{ref}}^r = kqQ\jäljellä.,\]

– Emme voi ottaa toinen termi on mielivaltainen jatkuva vertailutaso, joka toimii nollakohta:

\

kätevä valinta viite, joka perustuu meidän järkeä on, että kun kaksi maksut ovat äärettömän kaukana toisistaan, ei ole vuorovaikutusta niiden välillä. (Palauttaa mieliin keskustelun potentiaalienergian vertailupotentiaalista Potentiaalienergiassa ja energiansäästössä.,) Ottaen mahdolliset energia tämän valtion olevan nolla poistaa termi \(U_{ref}\) yhtälöstä (aivan kuten kun sanomme, että maa on nolla potentiaali energiaa painovoiman potentiaalienergia ongelma), ja potentiaalienergia Q, kun se on erotettu q etäisyyden r oletetaan muodossa,

\

Koska Coulombin laki, voimien vuoksi useita maksuja testi ilmaiseksi \(Q\) päällekkäin; ne voidaan laskea yksittäin ja sitten lisätty. Tämä merkitsee sitä, että työintegraalit ja siten tuloksena olevat potentiaaliset energiat osoittavat samaa käyttäytymistä., Tämän osoittamiseksi pidämme esimerkkinä neljän maksun järjestelmän kokoamista.

Huomaa, että sähköinen potentiaali energia on positiivinen, jos kaksi maksut ovat samaa tyyppiä, joko positiivinen tai negatiivinen, ja negatiivinen, jos kaksi maksut ovat päinvastaisia tyyppejä. Tämä on järkevää, jos luulet, että muutos potentiaalienergia \(\Delta U\), kun tuot kaksi maksut lähemmäksi tai siirrä ne kauemmaksi toisistaan., Riippuen suhteellisista maksutyypeistä, saatat joutua työskentelemään järjestelmän tai järjestelmä toimisi sinua, eli työsi on joko positiivinen tai negatiivinen. Jos täytyy tehdä positiivista työtä järjestelmän (itse asiassa työntää maksuja lähemmäksi), niin energian järjestelmän pitäisi kasvaa. Jos tuo kaksi positiivista tai kaksi negatiivista latausta lähemmäs, pitää tehdä positiivista työtä järjestelmän suhteen, mikä nostaa niiden potentiaalista energiaa. Koska potentiaalienergia on suhteessa 1 / r, potentiaalienergia nousee, kun r laskee kahden positiivisen tai kahden negatiivisen varauksen välillä.,

toisaalta,, jos et tuo positiivinen ja negatiivinen varaus lähemmäksi, sinun täytyy tehdä, negatiivinen työn järjestelmä (maksut ovat vetämällä sinua), mikä tarkoittaa, että voit ottaa energiaa pois järjestelmästä. Tämä vähentää potentiaalista energiaa. Koska potentiaalienergia on negatiivinen, jos positiivinen ja negatiivinen varaus, pari, kasvu 1/r tekee potentiaalienergia enemmän negatiivisia, joka on sama kuin vähentää mahdollisia energiaa.

esimerkin \(\PageIndex{2}\) tulosta voidaan laajentaa järjestelmiin, joissa on mielivaltainen määrä maksuja., Tässä tapauksessa, se on erittäin kätevä kirjoittaa kaava kuin

\

tekijä 1/2 tilejä lisäämällä kunkin parin maksuja kahdesti.