Hyvin epävirallisesti, kaksi termien summa antama Black-Scholes-kaava voi olla ajatellut kuin nykyinen hinta varastossa painotettu todennäköisyys, että voit käyttää teidän mahdollisuus ostaa varastossa ”miinus” alennettuun hintaan käyttäessään optio-painotettu todennäköisyys, että sinun tulee käyttää optiota’, tai yksinkertaisesti mitä aiot saada ”miinus” mitä aiot maksaa’ (Khan, 2013).,

Eurooppalainen myyntioptio (sopimusten oikeus, mutta ei velvollisuutta, myydä joitakin underlaying asset ennalta määrättyyn hintaan ennalta määritetty päivämäärä tulevaisuudessa) vastaa funktionaalinen muoto on:

Esimerkki: Lasketaan hinta Eurooppalainen osto-optio

jotta voitaisiin laskea, mitä hinta Eurooppalainen osto-optio pitäisi olla, me tiedämme, me tarvitsemme viisi edellyttämiä arvoja yhtälön 6 edellä. Ne ovat: 1. Osakkeiden nykyinen hinta (T), 2. Osto-option (X) harjoitushinta, 3. Viimeinen käyttöaika (T – t), 4. Riskitön korko (r) ja 5., Kannan volatiliteetti, joka saadaan historiallisten lokituottojen keskihajonnalla (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

Voimme arvioida kaikki varastossa volatiliteetti tarkastelemalla sen historiallisia hintoja, tai jopa helpompaa, laskemalla toinen vaihtoehto hinnat saman kannan eri maturiteetti/eräpäivät (T) ja liikunta/lakko hinnat (X), jos tiedämme, että ne on asetettu mukaan Black-Scholes-malli. Tuloksena oleva arvo σ on luku 0-1, joka edustaa markkinoiden implisiittistä volatiliteettia osakkeelle., Tesla, tuolloin kirjallisesti tämän artikkelin, arvo oli keskimäärin noin 0.38 4-5 eri vaihtoehdon hinta on noin sama päättymistä/eräpäivä. Input osaksi yhtälö 6 edellä, huomaamme, että puhelun vaihtoehto olemme kiinnostuneita pitäisi olla hinnat jossain noin $7.

Implisiittinen volatiliteetti

Vaikka se on mielenkiintoista ymmärtää, miten valinnat liikkeeseenlaskijoiden saapuvat hinta niiden puhelun ja laittaa vaihtoehtoja, koska sijoittajien on vaikea ”eri mieltä” tällaisia hintoja, sinänsä, ja niin vaikea kääntää tätä tietoa osaksi käytännöllisiä investointi opinnäytetöitä.,

Voimme kuitenkin saada paljon milage ulos Black-Scholes-kaava, jos me sen sijaan kohdella hinta vaihtoehto (C tai P) tunnettu määrä/riippumaton muuttuja (löytyy katsomalla eri maturiteetti/eräpäivät T ja eri liikunta-hinnat X). Tämä siksi, että jos emme tee, Black-Scholes toimiva yhtälö työkalu auttaa meitä ymmärtämään, miten markkina-arvioiden volatiliteetti varastossa, joka tunnetaan myös implisiittinen volatiliteetti vaihtoehto. Tästä tiedosta voimme olla eri mieltä ja käydä kauppaa vastaan.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called ”continuous timeline instruments”), they are much more difficult to deal with that European options (”point in time instruments”)., Ensisijaisesti, koska optimaalinen liikunta politiikka vaikuttaa option arvoa, tämä on otettava huomioon, kun ratkaista Black-Scholes-osittainen differential yhtälö. Amerikkalaisille vaihtoehdoille Ei Black-Scholesin yhtälön mukaan ole olemassa tunnettuja ”suljetun muodon” ratkaisuja. Siellä on, kuitenkin, joitakin erityisiä tapauksissa:

• American soittaa vaihtoehtoja omaisuuseriä, jotka eivät maksa osinkoa (tai muita maksuja), Amerikkalaisen osto-option hinta on sama kuin Euroopan soittaa vaihtoehtoja. Tämä siksi, että optimaalinen harjoituspolitiikka tässä tapauksessa on olla käyttämättä tätä vaihtoehtoa.,
• kun on kyse amerikkalaisista osto-optioista, jotka maksavat yhden tunnetun osingon elinaikanaan, optio voi olla optimaalista käyttää aikaisin., Tällaisissa tapauksissa vaihtoehto voidaan optimaalisesti käyttää juuri ennen varastossa menee ex-osinko, mukaan esitetty ratkaisu suljetussa muodossa niin sanottu Roll-Geske-Whaley menetelmä (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

tarkista Ensin, jos se on optimaalinen käyttää mahdollisuutta aikaisin, tutkimalla, onko seuraava epätasa-arvo on täyttyvät:

S = osakkeen hinta X = toteutushinta, D₁ = osinko maksetaan, t = nykyinen päivämäärä, t₁ = päivämäärä, osingon maksu, T = viimeinen vaihtoehto.

Jos epätasa-arvo ei täyty, varhainen liikunta ei ole optimaalista., Jos C(・) on säännöllinen Black-Scholes-kaava Euroopan soittaa vaihtoehtoja ei-osinkoa maksava varastossa (eq x), arvo Amerikkalainen osto-optio on sitten antama versio samasta yhtälöstä, jossa osakkeen hinta (T) on diskontattu:

Jos epätasa-arvo on täyttyvät, varhainen harjoitus on optimaalinen ja arvo Amerikkalainen osto-optio on annettu seuraavat, kauhea sotku yhtälö (yritin rikkoa sitä ylös kunkin aikavälillä, jotta se olisi luettavissa):

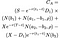
siinä Missä ennen S = hinta varastossa, T = voimassaoloajan päättymispäivä vaihtoehto, X = toteutushinta r = riskitön korko, σ = volatiliteetti (keskihajonta log historiallisen tuoton varastossa), ja D₁ on osingonmaksuun. Lisäksi, ρ lasketaan kaavasta:

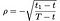
a₁, a₂ by:

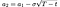
and b₁, b₂ by:

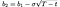
Rajoitukset

Sen pitäisi mennä ilman sanomalla, että Black-Scholes-malli on juuri se, teoreettinen malli, joka yrittää arvioida, miten markkinat käyttäytyy, koska oletukset edellä ja rajoituksensa oman numeeriset arviot riskittömien korkojen (r) ja tulevaisuuden volatiliteetti (σ). Tässä yhteydessä on korostettava, että kaikki (erityisesti alkuperäisen mallin) oletukset eivät itse asiassa ole empiirisesti päteviä., Esimerkiksi merkittäviä rajoituksia syntyy:

• aliarviointi äärimmäisiä liikkeitä varastossa, saadaan hännän riski
• olettaen, instant, kustannukset-vähemmän kaupankäynnin, saadaan likviditeettiriski
• oletus paikallaan prosessi, saadaan volatiliteetti riski
• oletus jatkuva aika-ja kauppa, saadaan kuilu riski

Nämä olisi otettava huomioon kaikki mahdolliset investointeja strategioita, esimerkiksi suojaamalla out-of-the-money-optiot, kaupankäynnin useita vaihtoja, suojausten kanssa volatiliteetti suojaus-ja Gamma-suojaus, vastaavasti.,

Taustatiedot

Mahdollisimman lyhyesti mainittu, että se oli Fischer Black ja Myron Scholes, joka vuonna 1973 osoitti, että dynaamisesti tarkistaa salkun tiettyjen sääntöjen mukaan poistaa odotettu tuotto kohde-etuutena olevia (Musta & Scholes, 1973). Heidän mallinsa on rakennettu aiemmin perustettuihin Bachelierin, Samuelsonin ja muiden teoksiin. Robert C. Merton oli ensimmäinen julkaista kirja laajentaa ymmärrystä malli ja kuka keksi termin ”Black-Scholes-hinnoittelu vaihtoehtoja-malli”., Scholes ja Merton sai vuoden 1997 Nobelin Memorial-Palkinnon taloustieteet niiden löytö menetelmä eroaa optio-oikeudet riski niiden taustalla olevia arvopapereita. Kun Fischer Black menehtyi vuonna 1995, hän ei olisi oikeutettu saamaan palkinnon, mutta oli tunnustettu tekijä, jonka Nobel-Akatemia.