Articles

Kommutatiiviset, assosiatiiviset ja Distributiiviset lait

by admin

Wow! Mikä sanahirviö! Mutta ideat ovat yksinkertaisia.

Kommutatiiviset lait

”Kommutatiiviset lait” sanovat, että voimme vaihtaa numeroita ja silti saada saman vastauksen …

… kun me lisätä:

a + b = b + a

Esimerkki:

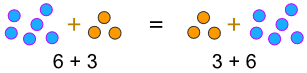
… tai kun me kerrotaan:

a × b = b × a

Esimerkki:

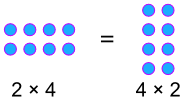
Kommutatiivinen Prosenttiosuudet!,

Koska a × b = b × a on myös totta, että a% b = b% a

Esimerkki: 8% 50 = 50% 8, joka on 4

Miksi ”kommutatiivinen” … ?

koska numerot voivat kulkea edestakaisin kuin työmatkalainen.

Assosiatiivinen Lait

”Assosiatiivinen Lait” sanoa, että se ei ole väliä, miten meidän ryhmä numeroita (eli joka me laskea ensin) …

…, kun me lisätä:

(a + b) + c = a + (b + c)

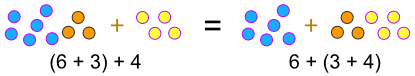
…,r>

Tästä: (2 + 4) + 5 = 6 + 5 = 11 On sama vastaus kuin tämä: 2 + (4 + 5) = 2 + 9 = 11

Tästä: (3 × 4) × 5 = 12 × 5 = 60
On sama vastaus kuin tämä: 3 × (4 × 5) = 3 × 20 = 60

Käyttö:

Joskus se on helpompaa, voit lisätä tai moninkertaistaa eri järjestyksessä:

Mikä on 19 + 36 + 4?,

19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59

Tai järjestää hieman:

Mikä on 2 × 16 × 5?

2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160

Jakelu Laki

”Distributive Law” on PARAS kaikista, mutta vaatii huolellista huomiota.,

Tämä on, mitä se antaa meidän tehdä:

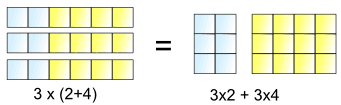
3 paljon (2+4) on sama kuin 3 paljon 2 plus 3 paljon 4

Joten, 3 x voi olla ”jaetaan” koko 2+4, 3×2-ja 3×4

Ja me kirjoittaa sen näin:

a × (b + c) = a × b + a × c

Yritä laskelmat itseltäsi:

  • 3 × (2 + 4) = 3 × 6 = 18
  • 3×2 + 3×4 = 6 + 12 = 18

kummallakin tavalla saa saman vastauksen.,

englanti voimme sanoa:

Saamme saman vastauksen kun meillä:

  • kerrotaan numero joukko numeroita lasketaan yhteen, tai
  • tehdä kunkin kerrotaan erikseen sitten lisää niitä

Käyttötarkoitukset:

Joskus se on helpompi hajottaa vaikea kerto:

Esimerkki: Mikä on 6 × 204 ?

6 × 204 = 6×200 + 6×4
= 1,200 + 24
= käsitti 1 224

Tai yhdistää:

Esimerkki: Mikä on 16 × 6 + 16 × 4?,

16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160

Voimme käyttää sitä vähennyslasku liian:

Esimerkki: 26×3 – 24×3

26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6

voisimme käyttää sitä pitkään luettelo lisäykset, liian:

Esimerkki: 6×7 + 2×7 + 3×7 + 5×7 + 4×7

6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140

. . . mutta älä mene liian pitkälle!,

Kommutatiivinen Laki ei toimi yhteen -, vähennys -, tai jako:

Esimerkki:

  • 12 / 3 = 4, mutta
  • 3 / 12 = ¼

Assosiatiivisia Laki ei toimi yhteen -, vähennys -, tai jako: