Tasasivuisen Kolmion Muotoinen

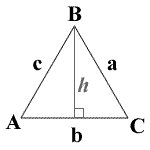
A = kulma
a = puolella
B = kulma B
b =, b-puolen
C = kulma C
c = puolella c
A = B = C = 60°
a = b = c
K = alue
P = kehä
s = semiperimeter
h = korkeus

*Pituus yksiköt ovat vain viitteellisiä, koska arvo jolloin pituudet ovat aina samat riippumatta siitä, mitä yksiköitä ovat.,

Laskimen Käyttö

tasasivuinen kolmio on erikoistapaus kolmio, jossa kaikki 3 osapuolet ovat yhtä pitkät ja kaikki 3 kulmat ovat tasa-arvoisia 60 astetta. Korkeus H on HB tai, korkeus B. tasasivuisten kolmioiden h = ha = HB = hc.

Jos sinulla on jokin 1 tunnettu, voit löytää loput 4 tuntematonta. Joten jos tiedät pituus on puoli = a, tai kehä = P, tai semiperimeter = s, tai ala = K, tai korkeus = h, voit laskea muita arvoja. Alla on 5 eri valintoja laskelmat voit tehdä tämän tasasivuinen kolmio laskin., Kerro meille, jos sinulla on muita ehdotuksia!, K-ja s

Koska alue löytää puoli, kehä, semiperimeter ja korkeus

• K on tiedossa, löytää, P -, s-ja h
• a = √ = 2 * √
• P = 3a
• s = 3 / a / 2
• s = (1/2) * √3 * a

Koska korkeuden löytää puoli, kehä, semiperimeter ja alueella

• s on tiedossa, löytää, P, s-ja K
• a = (2 / √3) * h
• P = 3a
• s = 3 / a / 2
• K = (1/4) * √3 * a2

lisätietoja kolmiot nähdä: