Yksinkertaiset koneet-miten pyörät ja akselit toimivat?
Eugene on pätevä ohjaus/instrumentointi-insinööri, Bsc (Eng) ja on työskennellyt kehittäjänä elektroniikka & ohjelmisto, SCADA-järjestelmät.

Kärrynpyörä
.,com
Pyörä ja Akseli — Yksi Kuudesta Klassisesta Simple Machines
Pyörät ovat kaikkialla meidän modernin teknologian yhteiskunnassa, mutta ne on myös käytetty antiikin ajoista lähtien. Paikka, jossa pyörän näkee todennäköisimmin, on ajoneuvossa tai perävaunussa, mutta pyöriä käytetään moniin muihin käyttökohteisiin. Niitä käytetään laajalti koneissa vaihteiden, hihnapyörien, laakereiden, telojen ja saranoiden muodossa. Pyörä luottaa vipuun kitkan vähentämiseksi.,
pyörä ja akseli on yksi kuudesta klassisen yksinkertaisia koneita määritelty Renessanssin tutkijat, joka sisältää myös vipu, väkipyörä, kiila, kalteva taso ja ruuvi.
ennen kuin luet tämän selityksen, josta tulee hieman tekninen, olisi hyödyllistä lukea toinen aiheeseen liittyvä artikkeli, jossa selitetään mekaniikan perusteet.,
Voima, Massa, Kiihtyvyys ja Miten Ymmärtää Newtonin Lait Liikkeen
Historia Wheel
Pyörät olivat tuskin on keksitty vain yksi henkilö, ja luultavasti kehitetty monia sivilisaatioita itsenäisesti yli vuosituhansien. Voimme vain kuvitella, miten se tapahtui. Ehkä joku kirkas kipinä huomasi, miten helppoa oli liu ’ uttaa jotain maahan pyöristetyillä kivikivillä, tai havaitsi, miten helposti puunrungot voitiin rullata, kerran kaataa. Ensimmäiset ”pyörät” olivat todennäköisesti puunrungoista tehtyjä teloja, jotka sijoitettiin raskaiden kuormien alle., Ongelma rullat on, että ne ovat pitkiä ja raskaita, ja niiden on oltava jatkuvasti uudelleen sijoitettava kuorman alle, joten akseli oli keksitty järjestää ohuempi levy, tehokkaasti pyörän tilalle. Varhaiset Pyörät tehtiin todennäköisesti kivestä tai litteistä laudoista, jotka yhdistettiin yhteen levyn muotoon.
Hetki Voima
ymmärtää, miten pyörät ja vivut toimi, meidän täytyy ymmärtää käsitteen hetkellä voimassa. Hetki voima asiasta, on suuruus ja voima kerrottuna kohtisuora etäisyys pisteen viiva voima.,
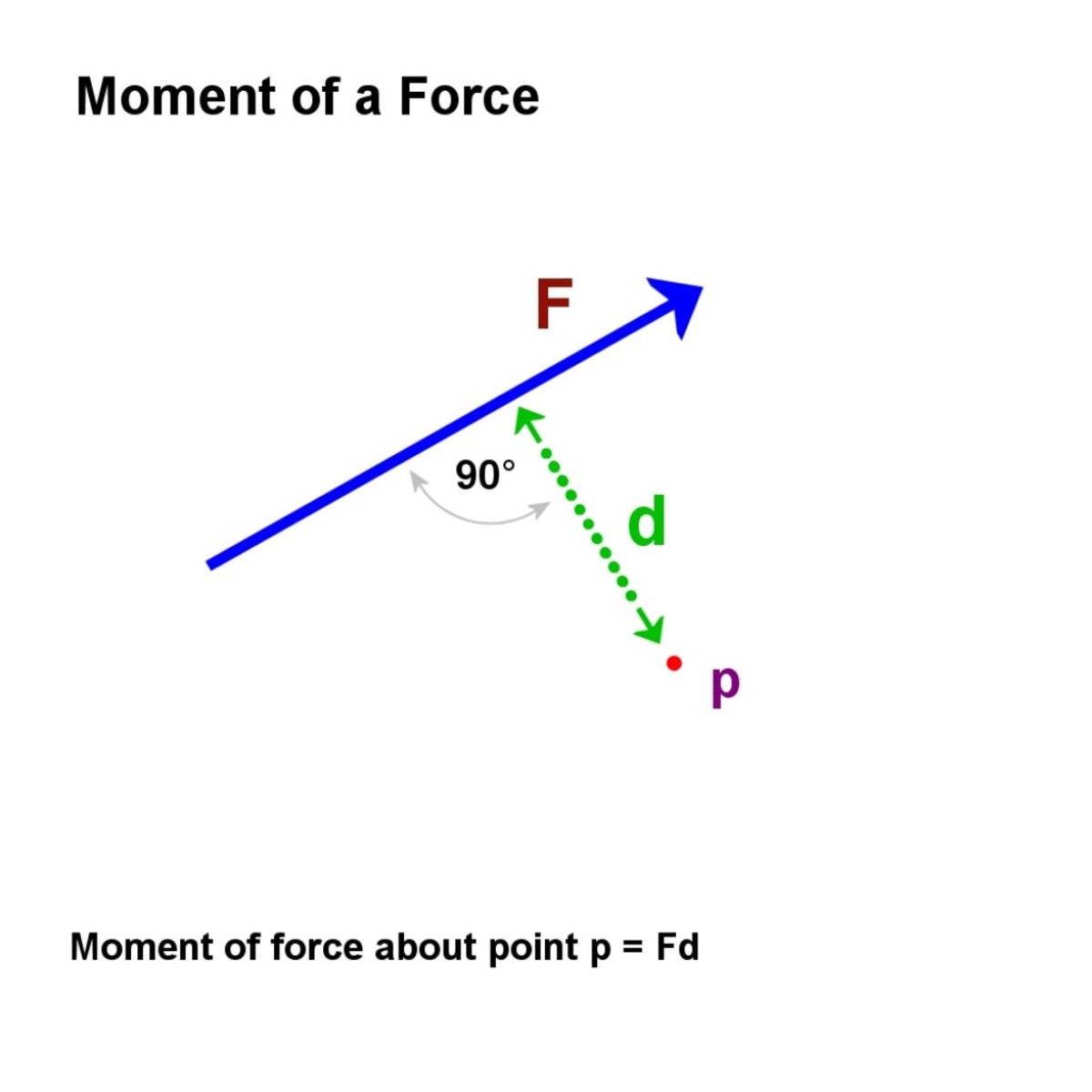
Hetki voima.
Kuva © Eugbug
Miksi Pyörät, jotta se on Helpompi ajaa Asioita?
kaikki kiteytyy kitkan vähentämiseen. Kuvittele, jos painosi lepää maassa. Newtonin 3. laki sanoo, että”jokaista toimintaa varten on yhtäläinen ja vastakkainen reaktio”. Kun siis yrität työntää kuormaa, voima siirtyy kuorman läpi pintaan, jonka päällä se lepää., Tämä on toimintaa. Vastaava reaktio on taaksepäin vaikuttavan kitkan voima ja riippuu sekä kosketuksessa olevien pintojen luonteesta että kuorman painosta. Tätä kutsutaan staattiseksi kitkaksi tai stictioniksi, ja se koskee kosketuksessa olevia kuivia pintoja. Aluksi reaktio vastaa toiminnan suuruus ja kuorma ei liiku, mutta lopulta jos painat tarpeeksi kovaa, kitka voima saavuttaa raja ja ei lisätä edelleen. Jos painat kovempaa, ylität rajoittavan kitkavoiman ja kuorma alkaa liukua., Kitkavoiman kuitenkin edelleen vastustaa liikettä (se vähentää hieman, kun liike alkaa), ja jos kuorma on erittäin raskasta ja/tai kosketuksiin joutuvat pinnat on korkea kitkakerroin, se voi olla vaikea liu ’ uttamalla sitä.
Pyörät poistavat tämän kitkavoiman käyttämällä vivutusta ja akselia. Ne tarvitsevat edelleen kitkaa, jotta ne voivat ”työntää takaisin” maassa, jolla ne rullaavat, muuten liukkaus tapahtuu. Tämä voima ei kuitenkaan vastusta liikettä tai vaikeuta pyörän pyörimistä.,
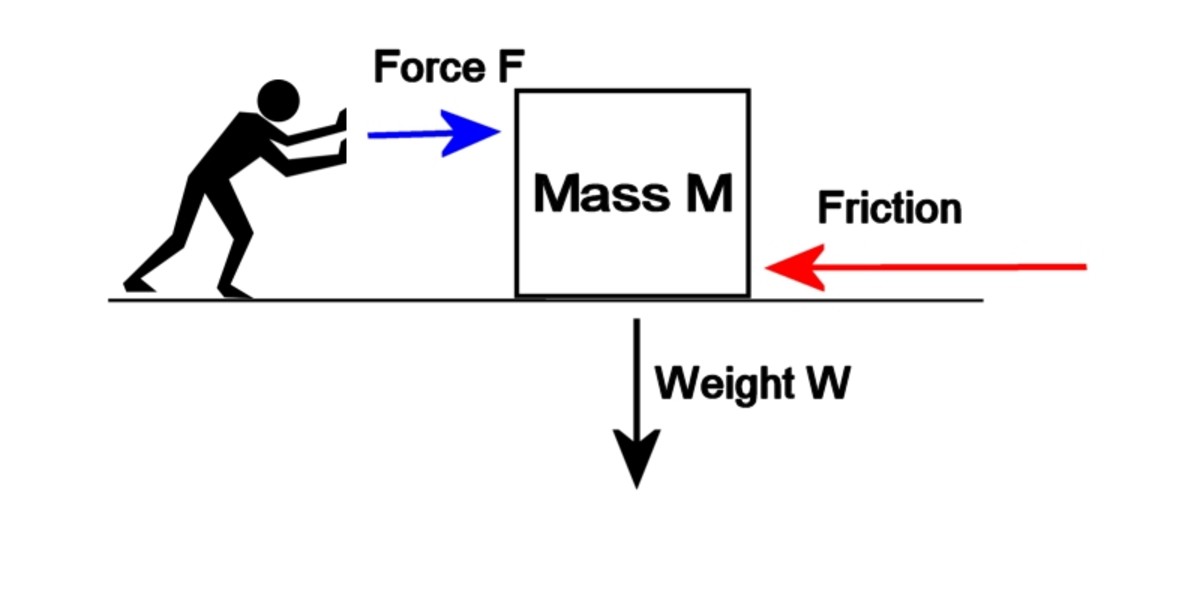
Friction can make sliding difficult
Image © Eugbug
Pushing a Cart With a Load – Wheels Make it Easier
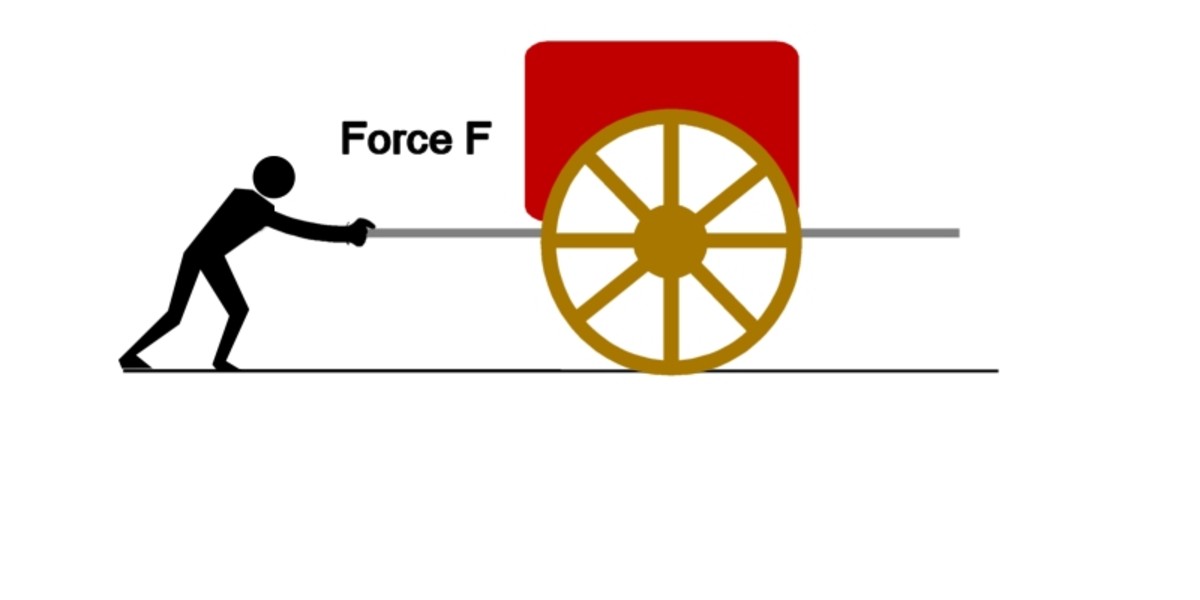
Pushing a cart with a load. Wheels make it easier
Image © Eugbug
How Do Wheels Work?,
Analyysi Pyörän, Koska Voimassa Akseli
Tämä analyysi koskee esimerkiksi edellä missä pyörä on asetettu voimaan tai vaivaa F akselin.
Kuva. 1
voima vaikuttaa akselin, jonka säde on d.
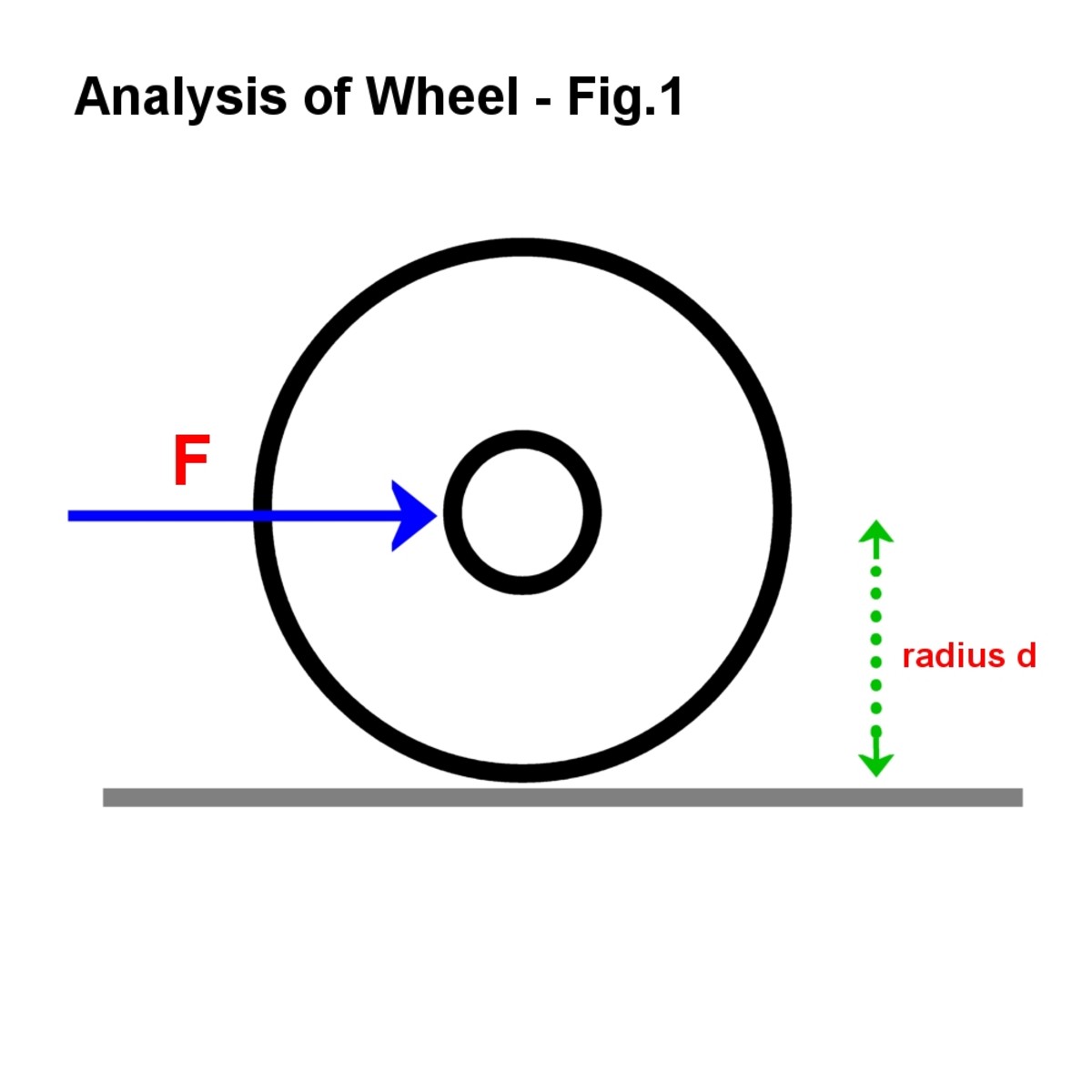
Kuva © Eugbug
Kuva. 2
Kaksi uutta tasa-arvoisia, mutta vastakkaiseen voimat ovat käyttöön jos pyörä täyttää pinnan., Tämä tekniikka lisäämällä kuvitteellisia voimia, jotka kumoavat toisensa, on hyödyllinen ongelmien ratkaisemisessa.
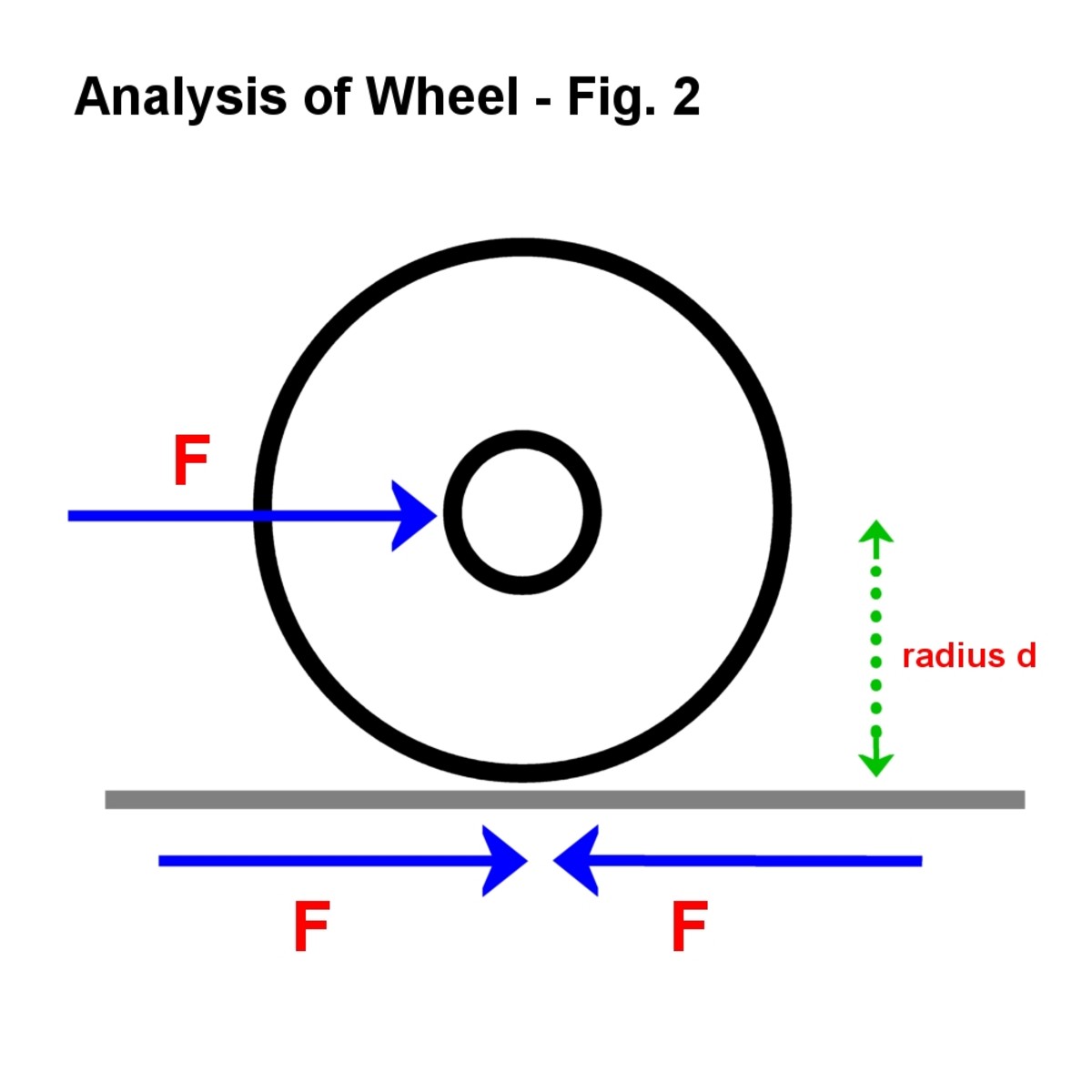
Lisää 2 kuvitteellisia voimia F
Kuva © Eugbug
Kuva. 3
kun kaksi voimaa toimii vastakkaisiin suuntiin, tulos tunnetaan parina ja sen suuruutta kutsutaan vääntömomentiksi. Kaaviossa lisätty voima johtaa pari plus aktiivinen voima, jossa pyörä täyttää pinnan., Tämän parin magnitudi on voima kerrottuna pyörän säteellä.
So Torque Tw = Fd.
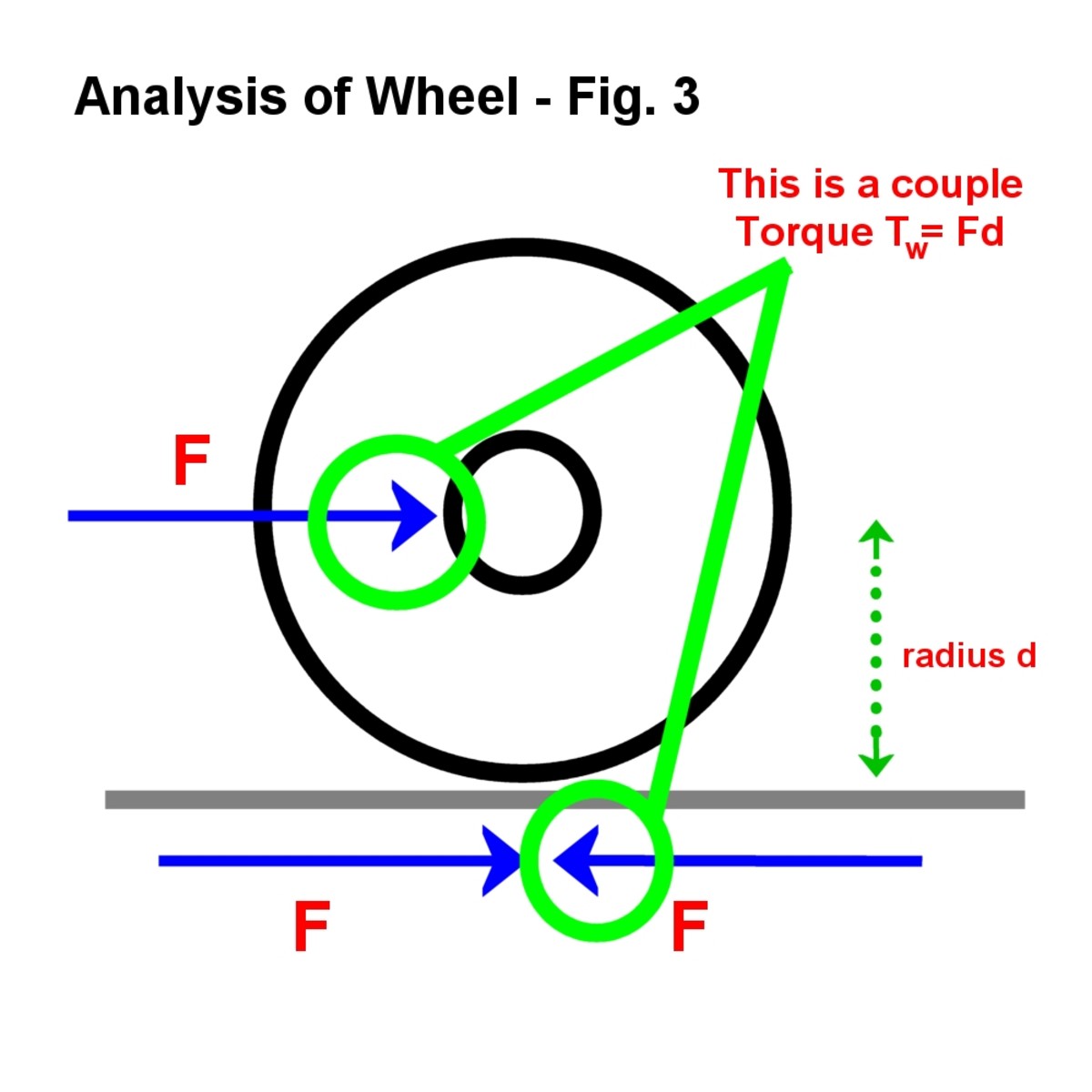
2 voimat muodostavat pari
Kuva © Eugbug
Kuva. 4
a lot is going on here! Siniset nuolet osoittavat aktiiviset voimat, violetti reaktiot. Kaksi sinistä nuolta korvannut vääntömomentti Tw toimii myötäpäivään., Jälleen Newtonin kolmas laki tulee peliin ja akselilla on rajoittava reaktiivinen vääntömomentti Tr. Tämä johtuu akselipainon aiheuttamasta kitkasta. Ruoste voi lisätä raja-arvoa, voitelu vähentää sitä.
Toinen esimerkki tästä on, kun yrität kumota mutteri joka on ruostunut kiinni pultti. Momenttia käytetään jakoavaimella, mutta ruoste sitoo mutterin ja toimii sinua vastaan. Jos käytät tarpeeksi vääntömomenttia, voit voittaa reaktiivisen vääntömomentin, jolla on raja-arvo. Jos mutteri on kunnolla kiinni ja käytät liikaa voimaa, pultti vääntyy.,
todellisuudessa asiat ovat monimutkaisempia ja siellä on tiedostojen reaktio johtuu hetkellä inertia pyörät, mutta ei pahenneta asioita ja olettaa, että pyörät ovat painoton!
- paino toimiva alas pyörän painosta johtuen cart on W.
- reaktio maan pinta on Rn = W
- Siellä on myös reaktio ratissa/pinta käyttöliittymä, koska voima F, joka toimii eteenpäin. Tämä ei vastusta liikettä, mutta jos se on riittämätön, pyörä ei käänny ja liukuu. Tämä on yhtä kuin F ja sen raja-arvo on FF = uurna.,
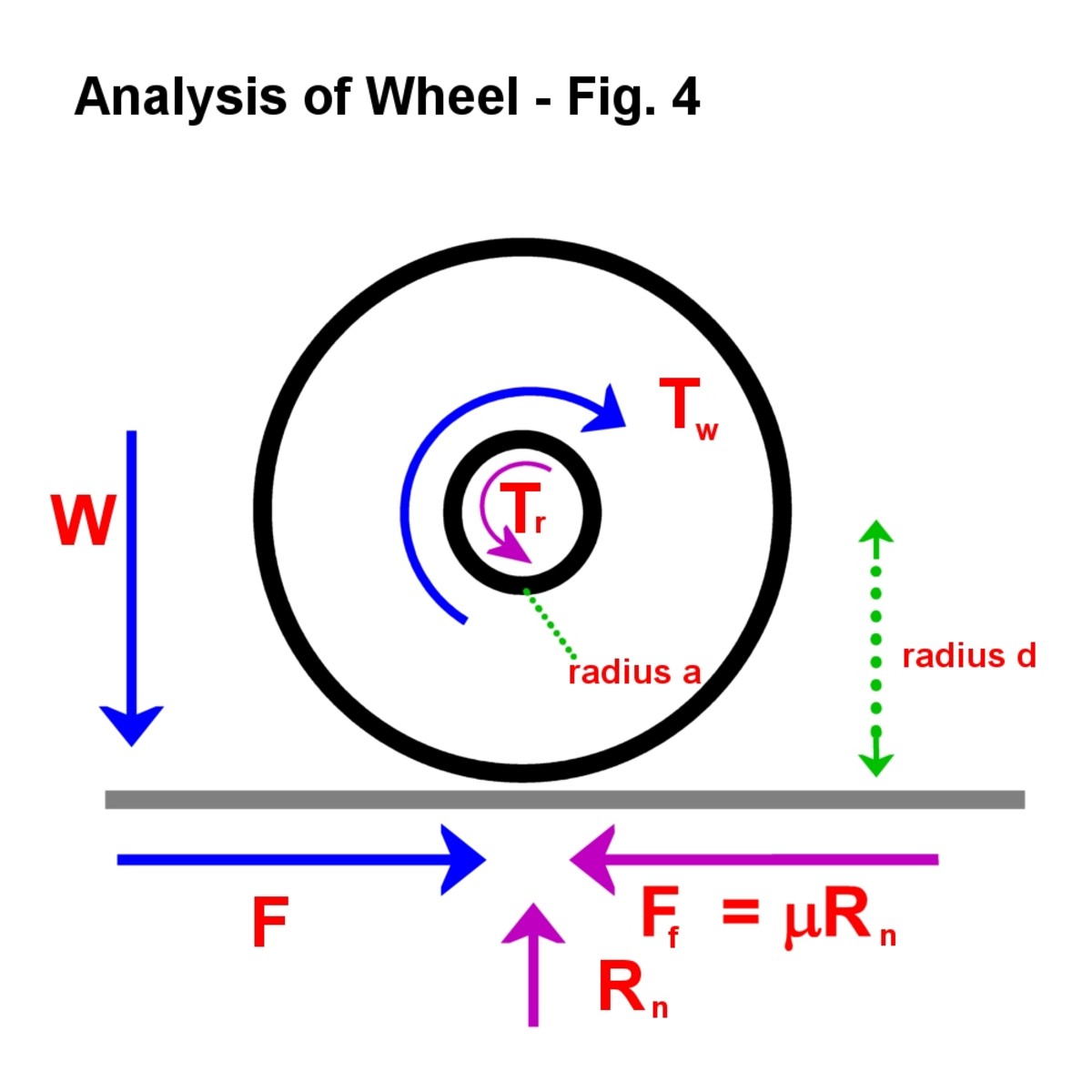
Reactions at the ground and axle
Image © Eugbug

Undoing a nut. The limiting value of friction must be overcome to release the nut
Image © Eugbug
Fig., 5
kaksi voimaa, jotka tuottavat vääntömomentin Tw, esitetään uudelleen. Nyt näet tämä muistuttaa vipujärjestelmä kuten edellä on selitetty. F vaikuttaa etäisyyden d yli, ja reaktio akselilla on Fr.
voima F suurenee akselilla ja näkyy vihreällä nuolella. Sen suuruus on:
Fe = F(d/a)
Koska suhde pyörän halkaisija akselin halkaisija on suuri , eli d/a-pienin voima F tarvitaan liike on suhteellisesti vähentynyt. Pyörän tehokkaasti toimii vipuna, suurennuslasi voimassa akseli, ja poistaa raja-arvo kitkavoima Fr., Huomautus myös tietyn akselin halkaisija a, Jos pyörän halkaisija on suurempi, Fe tulee suurempi. Isoilla pyörillä on siis helpompi painaa kuin pienillä pyörillä, koska akselilla on suurempi voima kitkan voittamiseksi.
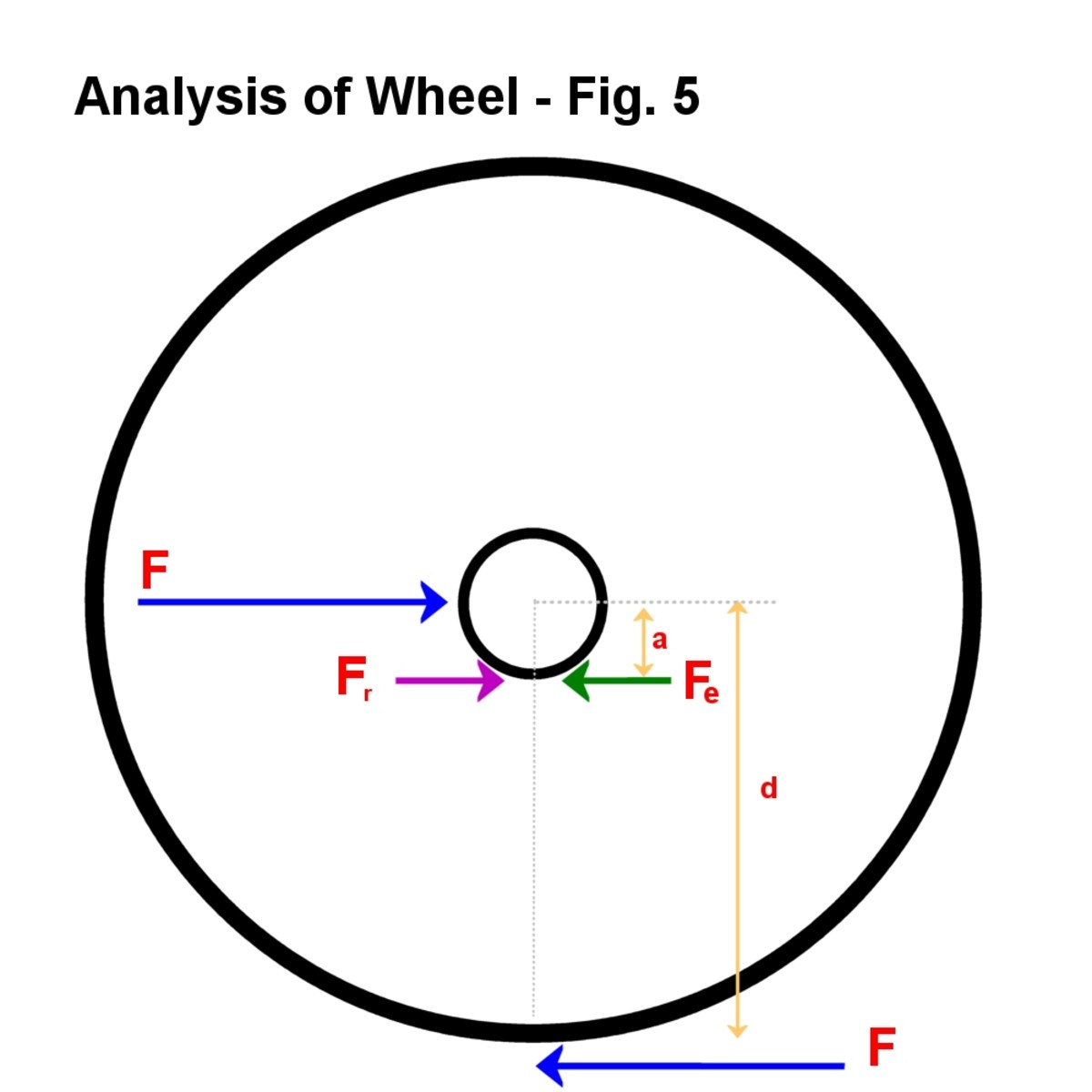
aktiiviset ja reaktiivisen voimat akselille
Kuva © Eugbug
Mikä on Parempi, Isot Pyörät tai Pienet Pyörät?,
Koska
Vääntömomentti = Voima x-Akselin Säde Pyörän
tietyn voima-akseli, vääntömomentti toimii tällä akseli on isompi isompi pyörät. Joten kitka akselilla on suuresti voittaa, ja siksi on helpompi työntää jotain isommilla pyörillä. Myös jos pinta, että pyörä rullaa ei ole kovin tasainen, suurempi halkaisija pyörät ovat yleensä sillan puutteita, mikä myös vähentää ponnistus.,
Kun pyörä on ajaa akselin, koska
Vääntömomentti = Voima x-Akselin Säde Pyörän
siksi
Voima-Akseli = Vääntömomentti / Säde Pyörän
Joten jatkuva ajo vääntö, pienempi halkaisija pyörät tuottavat enemmän vetävän vaivaa tällä akseli kuin suuremmat pyörät. Tämä on voima, joka työntää ajoneuvoa.
kysymykset & vastaa
kysymykseen: miten pyörä vähentää ponnistusta?
Vastaus: Se poistaa kineettinen kitka, joka vastustaa eteenpäin, kun kohde on liukui ja korvaa sen kitka-akseli/pyörä pelaajan., Pyörän halkaisijan kasvattaminen vähentää tätä kitkaa suhteessa.















