Nagyon informális, a két fogalom az összeget, mivel a Black-Scholes képlet lehet úgy, mint a jelenlegi ár a súlyozott állomány a valószínűsége, hogy gyakorolja a lehetőséget, hogy vásárolni a tőzsdei’ negatív ‘, a kedvezményes ár gyakorlása a lehetőséget, súlyozva a valószínűsége, hogy gyakorolja a lehetőség’, vagy egyszerűen csak ‘mi az lesz, hogy a’ negatív ‘, hogy mit fogsz fizetni’ (Khan, 2013).,

Az Európai eladási opció (szerződések joga, de nem kötelezettsége, hogy eladni néhány underlaying eszköz egy előre meghatározott áron, egy előre meghatározott dátuma, a jövőben) az azonos funkcionális forma:

példa: az Európai hívási opció árának kiszámítása

annak kiszámításához, hogy mi legyen az Európai hívási opció ára, tudjuk, hogy a fenti 6.egyenletben öt értékre van szükségünk. Ezek: 1. Az állomány (ok) aktuális ára, 2. A hívás opció (X) gyakorlati ára, 3. A lejáratig eltelt idő (T – t), 4. A kockázatmentes kamatláb (r) és az 5., Az állomány volatilitása, amelyet a történelmi naplóbejegyzések szórása ad (σ).

bármely állomány volatilitását becsülhetjük meg a történelmi árak megfigyelésével, vagy még egyszerűbben, ugyanazon készlet más opciós árainak kiszámításával különböző lejárat/lejárati dátumokon (T) és gyakorlat / sztrájk árakon (X), ha tudjuk, hogy azokat egy fekete-Scholes modell szerint állították be. A kapott érték, σ, Egy 0 és 1 közötti szám, ami a piac vélelmezett volatilitását jelenti az állomány számára., A Tesla esetében a cikk írásakor az érték átlagosan körülbelül 0, 38 volt 4-5 különböző opciós áron ugyanazon lejárati/lejárati dátum körül. Input egyenlet 6 fenti, azt találjuk,hogy a hívás opció érdekli kell árak valahol $7.

Implikált volatilitás

Bár érdekes, hogy megértsük, hogyan az opciók kibocsátók megérkezik az ár a vételi, illetve eladási lehetőség, mivel a befektetők nehéz, hogy “nem értenek egyet” ilyen árak, per se, így nehéz leállítani ezt a tudást a támadható befektetési tézisek.,

mi azonban kap egy csomó milage ki a fekete-Scholes képlet, ha ehelyett kezelni az ár egy lehetőség (C vagy P), mint egy ismert mennyiség/független változó (talált nézi a különböző lejárat/lejárati dátum T és különböző gyakorlat árak X). Ez azért van, mert ha igen, a fekete-Scholes funkcionális egyenlet eszközévé válik, hogy segítsen megérteni, hogy a piac hogyan becsüli meg az állomány volatilitását, más néven az opció implikált volatilitását. Ez olyan információ, amivel nem értünk egyet, és ellene kereskedünk.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called “continuous timeline instruments”), they are much more difficult to deal with that European options (“point in time instruments”)., Elsősorban, mivel az optimális gyakorlati politika befolyásolja az opció értékét, ezt figyelembe kell venni a fekete-Scholes részleges differenciálegyenlet megoldásakor. A fekete-Scholes-egyenlet szerint nincsenek ismert” zárt formájú ” megoldások Az Amerikai lehetőségekre. Vannak azonban néhány különleges eset:

• az olyan mögöttes eszközök amerikai hívási opciói esetében, amelyek nem fizetnek osztalékot (vagy más kifizetéseket), az amerikai hívási opció ára megegyezik az Európai hívási lehetőségekkel. Ez azért van, mert ebben az esetben az optimális gyakorlati politika az, hogy ne gyakorolja a lehetőséget.,
• az olyan mögöttes eszközök amerikai hívási opciói esetén, amelyek élettartama alatt egy ismert osztalékot fizetnek, optimális lehet a lehetőség korai gyakorlása., Ilyen esetekben a lehetőséget, lehet, hogy optimálisan gyakorolni, mielőtt a raktáron megy ex-dividend szerint megoldást adott a zárt forma az úgynevezett Roll-Geske-Whaley módszer (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

Először is, ellenőrizze, hogy az optimális gyakorolni a lehetőséget, korán, megvizsgálva, hogy a következő egyenlőtlenség teljesül:

mert S = részvényárfolyam, X = gyakorlati ár, D₁ = fizetett osztalék, t = aktuális dátum, t₁ = osztalékfizetés dátuma, T = opció lejárati dátuma.

Ha az egyenlőtlenség nem teljesül, korai gyakorlat nem optimális., Ha C(・) a rendszeres Black-Scholes képlet Európai hívás lehetőséget nem osztalékot fizető részvények (eq x), az érték, az Amerikai hívás lehetőséget, majd adott egy változata az azonos egyenlet, ahol a raktáron ár (Ek) kedvezményes:

Ha az egyenlőtlenség teljesül, a korai edzés optimális, de az értékét az Amerikai hívás lehetőséget adott a következő, szörnyű rendetlenség egyenlet (próbáltam abbahagyni az egyes kifejezés, hogy olvashatóbb legyen):

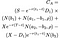
ahol, mint korábban s = a készlet ára, t = az opció lejáratának dátuma, X = gyakorlat ára és r = kockázatmentes kamatláb, σ = volatilitás (az állomány történelmi hozamának standard eltérése), D₁ pedig az osztalék kifizetése. Ezen felül ρ a következő:

a₁, a₂ by:

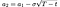
and b₁, b₂ by:

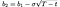
korlátozások

magától értetődik, hogy a Black-Scholes modell pontosan az, egy elméleti modell, amely megpróbálja megbecsülni, hogyan viselkedik a piac, tekintettel a fent említett feltételezésekre, valamint a kockázatmentes kamatlábak (R) és a jövőbeli volatilitás (σ) saját numerikus becsléseinek rejlő korlátaira. Itt ki kell emelni, hogy az összes feltételezése (különösen az eredeti modell) valójában empirikusan érvényes., Például, jelentős korlátai abból erednek, hogy:

• A alábecsült extrém mozog a raktáron, így farok kockázat
• A feltételezés, instant, költség-kevesebb, kereskedelmi, így likviditási kockázat
• A feltételezés, hogy egy álló folyamat, így a volatilitás a kockázat
• az a feltételezés, A folyamatos idő, valamint a kereskedelmi, hozamú gap kockázat

Ezek az kell elszámolni minden olyan befektetési stratégiákat, például a fedezeti out-of-the-money opciók kereskedési több cserék, fedezeti a volatilitás fedezeti, illetve Gamma fedezeti, ill.,

háttér

röviden megemlítve Fischer Black és Myron Scholes volt az, aki 1973-ban megmutatta, hogy a Portfólió dinamikus felülvizsgálata bizonyos szabályok szerint eltávolítja az alapul szolgáló biztonság várható visszatérését (Fekete & Scholes, 1973). Modelljük a Bachelier, Samuelson és mások által korábban létrehozott művekre épült. Robert C. Merton volt az első, aki megjelentetett egy tanulmányt, amely a modell megértéséről szólt, És aki megalkotta a “fekete-Scholes opciók árazási modellje”kifejezést., Scholes és Merton az 1997-es gazdasági Nobel-Emlékdíjat kapta azért, hogy felfedezték a részvényopciók elválasztásának módját az alapul szolgáló értékpapírok kockázatától. Mivel Fischer Black 1995-ben elhunyt, nem vehette át a díjat, hanem a Nobel-Akadémia közreműködőjeként ismerték el.