ha egyetemre jár, valószínűleg legalább néhány hallgatói szervezetben vett részt. Kezdem az 1. félévet, mint egy végzős hallgató Rochester Tech, és több mint 350 szervezetek itt. Különböző kategóriákba vannak rendezve a hallgató érdekei alapján. Mi határozza meg ezeket a kategóriákat, és ki mondja, hogy melyik org melyik kategóriába tartozik? Biztos vagyok benne, hogy ha megkérdeznéd az ilyen szervezeteket működtető embereket, nem mondanák, hogy az org-juk olyan, mint valaki más org-je, de valamilyen módon tudod, hogy hasonlóak., A testvériségeknek és a diákszövetségeknek ugyanaz az érdekük a görög élet iránt. A futball és a klubtenisz egyaránt érdeklődik a sport iránt. A Latino csoport és az ázsiai-amerikai csoport egyaránt érdeklődik a kulturális sokszínűség iránt. Lehet, hogy ha megméri az ilyen orgok által vezetett eseményeket és találkozókat, akkor automatikusan kitalálhatja, hogy melyik kategóriába tartozik egy szervezet. A hallgatói szervezetek segítségével elmagyarázom a K-legközelebbi szomszédok néhány fogalmát, vitathatatlanul a legegyszerűbb gépi tanulási algoritmus. A modell felépítése csak a képzési adatkészlet tárolásából áll., Egy új adatpont előrejelzéséhez az algoritmus megtalálja a legközelebbi adatpontokat a képzési adatkészletben-a “legközelebbi szomszédai”.”

hogyan működik

legegyszerűbb verziójában a k – NN algoritmus csak egy legközelebbi szomszédot vesz figyelembe, amely a legközelebbi képzési adatpont arra a pontra, amelyre előrejelzést akarunk készíteni. Az előrejelzés ezután egyszerűen a képzési pont ismert kimenete., Alábbi ábra szemlélteti ezt az esetben, ha a besorolás a forge adatbázis:

Itt adtunk három új adatokat, látható, mint a csillagok. Mindegyikük esetében megjelöltük a képzési készlet legközelebbi pontját. Az egy legközelebbi szomszéd algoritmus előrejelzése az adott pont címkéje (a kereszt színe mutatja).

ahelyett, hogy csak a legközelebbi szomszédot vesszük figyelembe, a szomszédok tetszőleges számát, k-t is figyelembe vehetjük., Ez az, ahol a neve a K-legközelebbi szomszédok algoritmus származik. Ha egynél több szomszédot veszünk figyelembe, akkor a szavazással címkét rendelünk hozzá. Ez azt jelenti, hogy minden egyes tesztpontnál számoljuk, hogy hány szomszéd tartozik a 0. osztályba, és hány szomszéd tartozik az 1. osztályba. Ezután hozzárendeljük a gyakoribb osztályt: más szóval a többségi osztályt a K-legközelebbi szomszédok között., A következő példa az öt legközelebbi szomszédot használja:

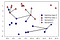
ismét az előrejelzés a kereszt színeként jelenik meg. Láthatjuk, hogy a bal felső sarokban lévő új adatpont előrejelzése nem ugyanaz, mint az előrejelzés, amikor csak egy szomszédot használtunk.

bár ez az ábra egy bináris osztályozási probléma, ez a módszer lehet alkalmazni adathalmazok tetszőleges számú osztályok., Több osztály esetében számoljuk, hogy hány szomszéd tartozik minden osztályhoz, majd ismét megjósoljuk a leggyakoribb osztályt.,könnyítése érdekében,

A Python kódot a funkció ki van itt:

ássunk egy kicsit mélyebbre a kódot:

• A funkció knnclassify veszi 4 bemenet: a bemeneti vektor, hogy osztályozza az úgynevezett teljes mátrix képzés példák úgynevezett adatkészlet egy vektor a címkék nevű címke, k — a számot a legközelebbi szomszédok, hogy használja a szavazati., A címkevektornak annyi elemnek kell lennie benne,mint az adatkészlet mátrixában.
• az A és az aktuális pont közötti távolságokat az euklideszi távolság alapján számítjuk ki.
• ezután növekvő sorrendben rendezzük a távolságokat.
• a Következő, a legkisebb k távolságok használják, hogy a szavazás az osztály A.
• Után miénk a classCount szótár pedig lebontják a listát a hármas sort, majd a párok a 2 elem a vektor. A fajta fordított, így a legnagyobb a legkisebb.,
• végül visszatérünk a leggyakrabban előforduló elem címkéjéhez.

a Végrehajtás Keresztül Scikit-Tanulni

Most vessünk egy pillantást, hogyan lehet végrehajtani a kNN algoritmus segítségével scikit-tanulni:

nézzük meg a kódot:

• Első, hozunk létre a írisz adatkészlet.
• ezután adatainkat egy képzési és tesztkészletre osztjuk, hogy értékeljük az általánosítási teljesítményt.
• ezután megadjuk a szomszédok számát (k) az 5-hez.
• ezután az osztályozót a képzési készlet segítségével illesztjük be.,
• a tesztadatokra vonatkozó előrejelzések készítéséhez az előrejelzési módszert nevezzük. A tesztkészlet minden adatpontjára a módszer a legközelebbi szomszédait számítja ki a képzési készletben, és megtalálja közöttük a leggyakoribb osztályt.
• végül értékeljük, hogy modellünk mennyire általánosítja a pontozási módszert tesztadatokkal és tesztcímkékkel.

a modell futtatása 97% – os pontosságot ad nekünk, ami azt jelenti, hogy a modell helyesen jósolta meg az osztályt a tesztadatkészletben szereplő minták 97% – ára.,

Erősségek, Gyengeségek

Alapvetően két fontos paramétereket a KNeighbors osztályozó száma szomszédok hogyan mérjük a távolságot adatok pontot.

• a gyakorlatban kis számú szomszéd, például három vagy öt gyakran jól működik, de ezt a paramétert biztosan be kell állítania.
• a megfelelő távolságmérő kiválasztása kissé trükkös., Alapértelmezés szerint euklideszi távolságot használnak, amely sok beállításban jól működik.

a k-NN egyik erőssége, hogy a modell nagyon könnyen érthető, gyakran ésszerű teljesítményt nyújt sok beállítás nélkül. Ennek az algoritmusnak a használata jó kiindulási módszer a kipróbálásra, mielőtt fejlettebb technikákat fontolgatna. A legközelebbi szomszédok modell építése általában nagyon gyors, de ha a képzési készlet nagyon nagy (akár a funkciók száma, akár a Minták száma), az előrejelzés lassú lehet. A K-NN algoritmus használatakor fontos az adatok előfeldolgozása., Ez a megközelítés gyakran nem teljesít jól a sok funkcióval rendelkező (több száz vagy annál több) adatkészleteknél, és különösen rosszul működik olyan adatkészleteknél, ahol a legtöbb funkció 0 (úgynevezett ritka adatkészletek).

összefoglalva

a K-legközelebbi szomszédok algoritmus egyszerű és hatékony módja az adatok osztályozásának. Ez egy példa a példány alapú tanulásra, ahol a gépi tanulási algoritmus végrehajtásához szükség van az adatok közelségére. Az algoritmusnak a teljes adathalmaz körül kell hordoznia; nagy adathalmazok esetén ez nagy mennyiségű tárolást jelent., Ezenkívül ki kell számítania az adatbázis minden adatának távolságmérését, ami nehézkes lehet. További hátrány, hogy a kNN nem ad semmilyen képet az adatok mögöttes szerkezetéről; fogalma sincs, hogy néz ki az egyes osztályok “átlagos” vagy “példa” példánya.

tehát, bár a legközelebbi k-szomszédok algoritmus könnyen érthető, nem gyakran használják a gyakorlatban, mivel a jóslat lassú, és nem képes kezelni számos funkciót.,

Referenciaforrások:

• Gépi tanulás Peter Harrington (2012)
• Bevezetés a gépi tanulásba a Python segítségével Sarah Guido és Andreas Muller (2016)