Quando un libero di carica positiva q è accelerato da un campo elettrico, si è dato l’energia cinetica (Figura \(\PageIndex{1}\))., Il processo è analogo a un oggetto che viene accelerato da un campo gravitazionale, come se la carica stesse scendendo una collina elettrica dove la sua energia potenziale elettrica viene convertita in energia cinetica, anche se ovviamente le fonti delle forze sono molto diverse. Esploriamo il lavoro svolto su una carica q dal campo elettrico in questo processo, in modo da poter sviluppare una definizione di energia potenziale elettrica.

La forza elettrostatica o Coulomb è conservativa, il che significa che il lavoro svolto su q è indipendente dal percorso intrapreso, come dimostreremo più avanti., Questo è esattamente analogo alla forza gravitazionale. Quando una forza è conservativa, è possibile definire un’energia potenziale associata alla forza. Di solito è più facile lavorare con l’energia potenziale (perché dipende solo dalla posizione) che calcolare direttamente il lavoro.

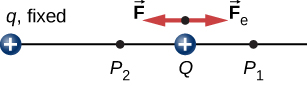
Il lavoro \(W_{12}\) fatto dalla forza applicata e \(\vec{F}\) quando la particella si sposta da \(1\) per \(P_2\) può essere calcolato mediante

\

\

in cui abbiamo definito positivo di puntare distanza dall’origine e r è la distanza dall’origine. Le direzioni sia dello spostamento che della forza applicata nel sistema in Figura \ (\PageIndex{2}\) sono parallele e quindi il lavoro svolto sul sistema è positivo.

Usiamo la lettera U per indicare l’energia potenziale elettrica, che ha unità di joule (J)., Quando una forza conservativa fa un lavoro negativo, il sistema guadagna energia potenziale. Quando una forza conservativa fa un lavoro positivo, il sistema perde energia potenziale, \(\Delta U = – W\). Nel sistema in Figura \(\PageIndex{3}\), la forza di Coulomb agisce nella direzione opposta allo spostamento; pertanto, il lavoro è negativo. Tuttavia, abbiamo aumentato l’energia potenziale nel sistema a due cariche.

In questo esempio, il lavoro svolto per accelerare una carica positiva dal riposo è positivo e deriva da una perdita in U o da un \negativo(\Delta U\)., Un valore per U può essere trovato in qualsiasi punto prendendo un punto come riferimento e calcolando il lavoro necessario per spostare una carica sull’altro punto.

L’energia potenziale gravitazionale e l’energia potenziale elettrica sono abbastanza analoghe. L’energia potenziale rappresenta il lavoro svolto da una forza conservatrice e fornisce informazioni aggiuntive sull’energia e sulla trasformazione dell’energia senza la necessità di trattare direttamente la forza. È molto più comune, ad esempio, utilizzare il concetto di energia potenziale elettrica piuttosto che affrontare la forza di Coulomb direttamente nelle applicazioni del mondo reale.,

\

Si noti che Q è una costante.

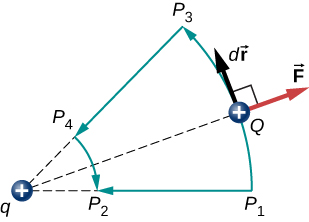
Un’altra implicazione è che possiamo definire un’energia potenziale elettrica. Ricordiamo che il lavoro svolto da una forza conservativa è anche espresso come la differenza nell’energia potenziale corrispondente a quella forza., Quindi, il lavoro \(W_{ref}\) per portare una carica da un punto di riferimento di un punto di interesse può essere scritto come:

\

e, dall’Equazione \ref{7.1}, la differenza di energia potenziale (\(U_2 – U_1\)) della carica di prova Q tra i due punti è di

\

Quindi, siamo in grado di scrivere una espressione generale per l’energia potenziale di due cariche puntiformi (in coordinate sferiche):

\_{r_{ref}}^r = kqQ\sinistra.,\]

Possiamo prendere il secondo termine come un livello di riferimento costante arbitrario, che funge da riferimento zero:

\

Una scelta conveniente di riferimento che si basa sul nostro buon senso è che quando le due cariche sono infinitamente distanti, non c’è interazione tra loro. (Ricordiamo la discussione sull’energia potenziale di riferimento in Energia potenziale e conservazione dell’energia.,) Prendendo l’energia potenziale di questo stato pari a zero e si rimuove il termine \(U_{ref}\) l’equazione (proprio come quando si dice che la terra è uguale a zero l’energia potenziale in energia potenziale gravitazionale problema), e l’energia potenziale di Q quando è separata dalla q da una distanza r assume la forma

\

a Causa della legge di Coulomb, le forze a causa di cariche multiple su una carica di prova \(Q\) sovrapporre; essi possono essere calcolati individualmente e poi aggiunto. Ciò implica che gli integrali di lavoro e quindi le energie potenziali risultanti mostrano lo stesso comportamento., Per dimostrare questo, consideriamo un esempio di assemblaggio di un sistema di quattro cariche.

si noti che il potenziale elettrico l’energia è positiva se le due cariche sono dello stesso tipo, positivo o negativo, e negativa se le due cariche sono di tipo opposto. Questo ha senso se pensi al cambiamento dell’energia potenziale \(\Delta U\) mentre avvicini le due cariche o le sposti più lontano., A seconda dei tipi relativi di oneri, potrebbe essere necessario lavorare sul sistema o il sistema avrebbe fatto il lavoro su di voi, cioè, il vostro lavoro è positivo o negativo. Se devi fare un lavoro positivo sul sistema (in realtà spingere le cariche più vicino), allora l’energia del sistema dovrebbe aumentare. Se porti due cariche positive o due cariche negative più vicine, devi fare un lavoro positivo sul sistema, che aumenta la loro energia potenziale. Poiché l’energia potenziale è proporzionale a 1 / r, l’energia potenziale sale quando r scende tra due cariche positive o due negative.,

D’altra parte, se avvicini una carica positiva e una negativa, devi fare un lavoro negativo sul sistema (le cariche ti stanno tirando), il che significa che togli energia dal sistema. Questo riduce l’energia potenziale. Poiché l’energia potenziale è negativa nel caso di una coppia di carica positiva e negativa, l’aumento di 1/r rende l’energia potenziale più negativa, che è la stessa di una riduzione dell’energia potenziale.

Il risultato dell’esempio \(\PageIndex{2}\) può essere esteso a sistemi con qualsiasi numero arbitrario di addebiti., In questo caso, è più conveniente scrivere la formula come

\

Il fattore di 1/2 rappresenta l’aggiunta di ogni coppia di cariche due volte.