Molto informalmente, i due termini della somma data dal Black-Scholes formula può essere pensato come ” l’attuale prezzo del titolo ponderata per la probabilità che si esercitare l’opzione per acquistare le azioni di’ meno ‘il prezzo scontato di esercitare l’opzione ponderata per la probabilità che si eserciterà l’opzione’, o, semplicemente, ‘che cosa avete intenzione di ottenere’ meno ‘che cosa avete intenzione di pagare ” (Khan, 2013).,

Per una opzione put Europea (contratti di diritto, ma non obbligo, di vendere alcuni asset sottostante a un prezzo prestabilito in una determinata data futura) l’equivalente funzionale del modulo è:

Esempio: Calcolo del prezzo di un’opzione call Europea

al fine di calcolare il prezzo di un’opzione call Europea dovrebbe essere, sappiamo che abbiamo bisogno di cinque valori richiesti dalla equazione 6 di cui sopra. Essi sono: 1. Il prezzo corrente delle azioni, 2. Il prezzo di esercizio dell’opzione call (X), 3. Il tempo di scadenza (T-t), 4. Il tasso di interesse privo di rischio (r) e 5., La volatilità del titolo, data dalla deviazione standard dei rendimenti log storici (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

Possiamo stimare la volatilità di qualsiasi titolo osservando i suoi prezzi storici, o, ancora più semplice, calcolando altri prezzi di opzione per lo stesso titolo a diverse scadenze/date di scadenza (T) e prezzi di esercizio / strike (X), se sappiamo che sono stati impostati secondo un modello Black-Scholes. Il valore risultante, σ, è un numero compreso tra 0 e 1, che rappresenta la volatilità implicita del mercato per il titolo., Per Tesla, al momento della stesura di questo articolo, il valore era in media di circa 0,38 per 4-5 diversi prezzi delle opzioni intorno alla stessa data di scadenza/scadenza. Input nell’equazione 6 sopra, troviamo che l’opzione call che ci interessa dovrebbe essere prezzi da qualche parte intorno a $7.

Volatilità implicita

Anche se è interessante capire come gli emittenti di opzioni arrivano al prezzo delle loro opzioni call e put, come investitori è difficile “non essere d’accordo” con tali prezzi, di per sé, e così difficile trasformare questa conoscenza in tesi di investimento attuabili.,

Possiamo comunque ottenere un sacco di milage dalla formula di Black-Scholes se invece trattiamo il prezzo di un’opzione (C o P) come una quantità nota/variabile indipendente (trovata osservando diverse date di scadenza / scadenza T e diversi prezzi di esercizio X). Questo perché, se lo facciamo, l’equazione funzionale Black-Scholes diventa uno strumento per aiutarci a capire come il mercato stima la volatilità di un titolo, noto anche come la volatilità implicita dell’opzione. Queste sono informazioni su cui possiamo non essere d’accordo e contro il commercio.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called “continuous timeline instruments”), they are much more difficult to deal with that European options (“point in time instruments”)., Principalmente, poiché la politica di esercizio ottimale influenzerà il valore dell’opzione, questo deve essere preso in considerazione quando si risolve l’equazione differenziale parziale di Black-Scholes. Non ci sono soluzioni conosciute di “forma chiusa” per le opzioni americane secondo l’equazione di Black-Scholes. Ci sono, tuttavia, alcuni casi speciali:

• Per le opzioni call americane su attività sottostanti che non pagano dividendi (o altri pagamenti), il prezzo dell’opzione call americana è lo stesso delle opzioni call europee. Questo perché la politica di esercizio ottimale in questo caso è di non esercitare l’opzione.,
• Per le opzioni call americane su attività sottostanti che pagano un dividendo noto nel corso della sua vita, potrebbe essere ottimale esercitare l’opzione in anticipo., In tali casi, l’opzione può essere esercitato in modo ottimale poco prima la stock va ex-dividendo, secondo una soluzione in forma chiusa dal cosiddetto Roll-Geske-Whaley metodo (Rotolo, 1977; Geske, 1979; 1981; Whaley, 1981):

in Primo luogo, verificare se è il momento ottimale per l’esercizio dell’opzione di anticipo, da indagare se la disequazione è soddisfatta:

Per S = prezzo delle azioni, X = prezzo di esercizio, d = = dividendo pagato, t = data corrente, t date = data di pagamento del dividendo, T = data di scadenza dell’opzione.

Se la disuguaglianza non è soddisfatta, l’esercizio precoce non è ottimale., Se C(・) è il regular Black-Scholes formula Europea opzioni call sul non-dividendo paganti stock (eq x), il valore dell’opzione call Americana è quindi dato da una versione di una stessa equazione in cui il prezzo del titolo (S) è scontato:

Se la disuguaglianza è soddisfatta, l’esercizio anticipato è ottimale e il valore dell’opzione call Americana, è dato dalla seguente, terribile, pasticcio di un’equazione (ho cercato di rompere ogni termine per renderlo più leggibile):

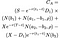
Dove come prima S = prezzo delle azioni, T = data di scadenza dell’opzione, X = prezzo di esercizio e r = tasso di interesse privo di rischio, σ = volatilità (deviazione standard del log dei rendimenti storici del titolo), e d is è il pagamento del dividendo. Inoltre, ρ è dato da:

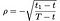
a₁, a₂ by:

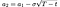
and b₁, b₂ by:

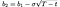
Limitazioni

Va da sé che il modello Black-Scholes è proprio questo, un modello teorico che cerca di stimare come si comporta un mercato, date le ipotesi sopra esposte e le limitazioni intrinseche delle nostre stime numeriche dei tassi di interesse privi di rischio (r) e della volatilità futura (σ). Va qui evidenziato che non tutte le ipotesi (in particolare il modello originale) sono in realtà empiricamente valide., Per esempio, significative limitazioni derivano da:

• La sottovalutazione di estrema si muove in stock, producendo coda di rischio
• L’assunzione immediata, costo meno di negoziazione, producendo rischio di liquidità
• L’assunzione di un processo stazionario, producendo volatilità rischio
• L’assunzione a tempo continuo e di negoziazione, producendo divario di rischio

Questi devono essere contabilizzate in qualsiasi e tutte le strategie di investimento, per esempio attraverso la copertura con out-of-the-money opzioni, trading su più scambi, di copertura, con la volatilità di copertura e la Gamma di copertura, rispettivamente.,

Background

Come accennato brevemente furono Fischer Black e Myron Scholes che nel 1973 mostrarono che la revisione dinamica di un portafoglio in base a determinate regole rimuove il rendimento atteso del titolo sottostante (Black& Scholes, 1973). Il loro modello costruito su opere precedentemente stabilite da Bachelier, Samuelson e altri. Robert C. Merton fu il primo a pubblicare un documento che ampliava la comprensione del modello e che coniò il termine “Black-Scholes options pricing model”., Scholes e Merton è stato assegnato il Premio Nobel per le scienze economiche 1997 per la loro scoperta del metodo di divorziare stock option dal rischio dei loro titoli sottostanti. Quando Fischer Black morì nel 1995, non avrebbe potuto ricevere il premio, ma fu riconosciuto come contributore dall’Accademia Nobel.