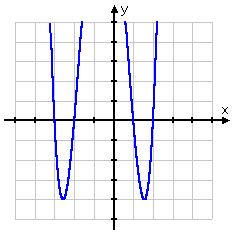
Le Radici Razionali di Prova
Torna all’Indice Lezioni | Fare le Lezioni in Ordine | versione stampabile della pagina
Le Radici Razionali di Prova: Introduzione (pagina 1 di 2)
zero di un polinomio è un valore in ingresso (di solito un valore di x) che restituisce un valore pari a zero per tutto il polinomio quando si collega in polinomiale. Quando uno zero è un numero reale (cioè non complesso), è anche un’intercetta x del grafico della funzione polinomiale., Spesso (specialmente nel calcolo) vorrai conoscere la posizione degli zeri di una data funzione polinomiale. Potresti inserire i numeri nel polinomio, volenti o nolenti, e sperare per il meglio. Ma come hai imparato quando hai studiato la Formula quadratica, gli zeri sono spesso numeri molto disordinati; indovinare casualmente non è probabilmente il miglior piano di attacco. Quindi, come si fa a cercare di trovare gli zeri?
Il test Rational Roots (o Rational Zeroes) è un modo pratico per ottenere un elenco di utili prime ipotesi quando si sta cercando di trovare gli zeri (radici) di un polinomio., Dato un polinomio con coefficienti interi (cioè “numeri interi” positivi e negativi), gli zeri possibili (o potenziali) si trovano elencando i fattori del termine costante (ultimo) sui fattori del coefficiente principale, formando così un elenco di frazioni. Questo elenco fornisce un elenco di potenziali radici razionali (frazionarie) da testare-da qui il nome del Test.
Permettetemi di sottolineare: Il test delle radici razionali non ti dà gli zeri. Non dice quali saranno sicuramente gli zeri., Il test ti fornisce solo un elenco di numeri relativamente facili e “belli” da provare nel polinomio. La maggior parte di questi possibili zeri si rivelerà in realtà non essere zeri!
Puoi vedere il senso della metodologia del Test osservando un semplice polinomio. Dato il quadratico 12×2-7x – 10, puoi usare la Formula quadratica per trovare gli zeri, ma puoi anche calcolare per ottenere 12×2 – 7x – 10 = (3x + 2)(4x-5). Impostando i due fattori uguali a zero, si ottengono due radici a x – – 2/3 e x = 5/4., Si noti che i denominatori “3” e “4” sono fattori del coefficiente principale “12” e i numeratori “2” e “5” sono fattori del termine costante “10”. Cioè, gli zeri sono frazioni formate da fattori del termine costante (10) rispetto ai fattori del coefficiente principale (12). Si noti inoltre, tuttavia, che frazioni come 5/6 e – 10/3 possono anche essere formate in questo modo (e quindi essere fornite dal Test), ma queste altre frazioni non sono in realtà zeri di questo quadratico.,
Questa relazione è sempre vera: se un polinomio ha radici razionali, allora quelle radici saranno frazioni della forma (più o meno) (fattore del termine costante) / (fattore del coefficiente principale). Tuttavia, non tutte le frazioni di questa forma sono necessariamente zeri del polinomio. In effetti, può accadere che nessuna delle frazioni così formate sia in realtà uno zero del polinomio.
Pubblicità
Nota che continuo a dire radici “potenziali”, “possibili” zeri”, se ci sono tali radici…”., Questo perché l’elenco delle frazioni generate dal test Rational Roots è solo un elenco di potenziali soluzioni. Non deve essere vero che nessuna delle frazioni è in realtà una soluzione. Potrebbero non esserci radici frazionarie! Ad esempio, dato x2 – 2, i test Rational Roots forniscono i seguenti possibili zeri razionali:
![]()
Ma sai già che:
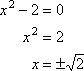
so quindi gli zeri non sono affatto razionali.,
Ricorda sempre: Il test Rational Roots fornisce solo una lista di buone prime ipotesi; NON ti dà “le” risposte!
- Trova tutte le possibili intercettazioni x razionali di x4 + 2×3-7×2 – 8x + 12.
|
Puoi fare un grafico veloce (specialmente se hai una calcolatrice grafica), e vedere che, fuori dall’elenco sopra, probabilmente sarebbe bene iniziare a cercare gli zeri inserendo i valori x = -3, -2, 1 e 2 nel polinomio., |
|
Top | 1 | 2 | Return to Index Next >>