Articles

Leggi commutative, associative e distributive

by admin

Wow! Che bocca piena di parole! Ma le idee sono semplici.

Leggi commutative

Le “Leggi commutative” dicono che possiamo scambiare i numeri e ottenere comunque la stessa risposta …

… quando aggiungiamo:

a + b = b + a

Esempio:

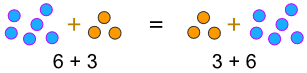
… o quando moltiplichiamo:

a × b = b × a

Esempio:

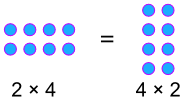
Percentuali commutative!,

Perché a × b = b × a è anche vero che una% di b = b% di un

Esempio: 8% di 50 = 50% 8, 4

Perché “commutativa” … ?

Perché i numeri possono viaggiare avanti e indietro come un pendolare.

Leggi associative

Le “Leggi associative” dicono che non importa come raggruppiamo i numeri (cioè che calcoliamo per primi) …

…, quando aggiungiamo:

(a + b) + c = a + (b + c)

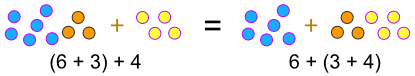
…,r>

Questo: (2 + 4) + 5 = 6 + 5 = 11 Ha la stessa risposta come questa: 2 + (4 + 5) = 2 + 9 = 11

Questo: (3 × 4) × 5 = 12 × 5 = 60
Ha la stessa risposta come questa: 3 × (4 × 5) = 3 × 20 = 60

Utilizzo:

a Volte è più facile per aggiungere o moltiplicare in un ordine diverso:

Quello che è 19 + 36 + 4?,

19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59

O per riorganizzare un po’:

Che cosa è 2 × 16 × 5?

2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160

Legge distributiva

La “Legge distributiva” è la MIGLIORE di tutte, ma richiede un’attenzione particolare.,

Questo è ciò che ci permette di fare:

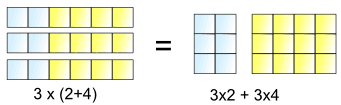
3 lotti di (2+4) è la stessa di 3 lotti di 2 plus 3 lotti di 4

Così, il 3× può essere “distribuiti” tra il 2+4, in 3×2 e 3×4

E si scrive così:

a × (b + c) = a × b + a × c

Provare i calcoli da soli:

  • 3 × (2 + 4) = 3 × 6 = 18
  • 3×2 + 3×4 = 6 + 12 = 18

in ogni modo si ottiene la stessa risposta.,

In inglese, si può dire:

Si ottiene la stessa risposta quando abbiamo:

  • moltiplicare un numero per un gruppo di numeri che sommati insieme, o
  • fare ogni moltiplicare separatamente per poi aggiungere

Usa:

a Volte è più facile rompere un difficile moltiplicazione:

Esempio: che Cosa è 6 × 204 ?

6 × 204 = 6×200 + 6×4
= 1,200 + 24
= 1,224

O per combinare:

Esempio: Che cosa è 16 × 6 + 16 × 4?,

16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160

Si può usare in sottrazione troppo:

Esempio: 26×3 – 24×3

26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6

potremmo utilizzarlo per un lungo elenco di aggiunte, troppo:

Esempio: 6×7 + 2×7 + 3×7 + 5×7 + 4×7

6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140

. . . ma non andare troppo lontano!,

La Legge Commutativa non funziona per sottrazione o divisione:

Esempio:

  • 12 / 3 = 4, ma
  • 3 / 12 = ¼

Associativo Legge non funziona per sottrazione o divisione: