非常に非公式には、Black-Scholes formulaによって与えられる和の二つの項は、”あなたが株式を購入するためにあなたのオプションを行使する確率によって重み付けされた株式の現在の価格”マイナス”あなたがオプションを行使する確率によって重み付けされたオプションを行使する割引価格”、または単に”あなたが得ようとしているもの”マイナス”あなたが支払うつもりであるもの”（Khan、2013）と考えることができる。,

ヨーロッパのプット-オプション（将来、事前に決定された日付に事前に決定された価格でいくつかの下にある資産を売却する権利であるが義務ではない契約）の場合、同等の機能形式は次のとおりです。

例:ヨーロッパのコール-オプションの価格の計算

ヨーロッパのコール-オプションの価格がどうあるべきかを計算するためには、上記の式6で必要とされる五つの値が必要であることがわかっています。 それらは:1. 株式の現在の価格(S),2. コールオプションの行使価格(X),3. 有効期限までの時間(T-t),4. リスクフリー金利（r）と5。, 過去ログリターンの標準偏差（σ）によって与えられる株式のボラティリティ。

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

ブラック-ショールズ-モデルに従って設定されていることがわかっていれば、過去の価格を観察することによって、または異なる満期日/有効期限（T）および行使価格/行使価格（X）で同じ株式の他のオプション価格を計算することによって、さらに簡単に、任意の株式のボラティリティを推定することができる。 結果の値,σ,間の数です0と1,株式のための市場のインプライド*ボラティリティを表します., テスラのために、この記事を書いている時点で、値は同じ有効期限/満期日の周りに約0.38の異なるオプション価格のために4-5で平均しました。 上記の式6に入力すると、興味のあるコールオプションは$7の周りの価格でなければなりません。

インプライド-ボラティリティ

それはオプション発行体が彼らのコールの価格に到着し、オプションを置く方法を理解することは興味深いですが、,投資家として、それはそのような価格に”反対”するのは難しいです,それ自体,そして実用的な投資論文にこの知識を有効にするのは難しいです.,しかし、オプション（CまたはP）の価格を既知の数量/独立変数（異なる満期/有効期限Tと異なる行使価格Xを見ることによって見つかる）として扱うと、Black-Scholes式から多くのマイラージを得ることができます。 これは、我々が行う場合、ブラック-ショールズ関数式は、私たちは市場がまた、オプションのインプライド*ボラティリティとして知られている株式のボラティ これは、私たちが反対し、取引することができる情報です。,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called “continuous timeline instruments”), they are much more difficult to deal with that European options (“point in time instruments”)., 主に、最適な運動ポリシーはオプションの値に影響するため、Black-Scholes偏微分方程式を解くときにこれを考慮する必要があります。 ブラック-ショールズ方程式によれば、アメリカのオプションに対する既知の”閉じた形”解は存在しない。 しかし、いくつかの特別なケースがあります：

• 配当（またはその他の支払い）を払っていない原資産のアメリカのコールオプションの場合、アメリカのコールオプションの価格はヨーロッパのコールオプションの場合と同じです。 これは、この場合の最適な運動方針がオプションを行使しないことであるためです。,
• その一生の間に一つの既知の配当を支払うん原資産のアメリカのコールオプションについては、早期にオプションを行使するのが最適かもしれ, このような場合、オプションは、いわゆるRoll-Geske-Whaley法（Roll、1977;Geske、1979;1981;Whaley、1981）によって閉じた形で与えられた解に従って、株式が配当落ちる直前に最適に行使される可能性があります。

まず、次の不等式が満たされているかどうかを調べることによって、オプションを早期に行使するのが最適かどうかを確認してください。

S=株価、x=行使価格、D÷=配当支払い、t=現在の日付、t÷=配当支払いの日付、t=オプションの有効期限。

不等式が満たされていない場合は、早期にそれを行使する最適ではありません。, C(・)が非配当株式（eq x）に関するヨーロッパのコールオプションの通常のブラック-ショールズ式である場合、アメリカのコールオプションの値は、株価が割引される同じ式のバージョンによって与えられます。

不等式が満たされている場合、早期演習が最適であり、American callオプションの値は次のように与えられます（読みやすくするために項ごとにそれを分割しようとしました）：

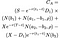
ここで、s=株式の価格、t=オプションの満了日、X=行使価格およびr=リスクフリー金利、σ=ボラティリティ（株式の履歴リターンのログの標準偏差）、 さらに、λは次のように与えられます。

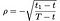
a₁, a₂ by:

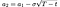
and b₁, b₂ by:

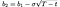
制限

ブラック-ショールズ-モデルは、上記の仮定と、リスクフリー金利（r）と将来のボラティリティ（θ）の数値推定の固有の限界を考えると、市場の振る舞いを推定しようとする理論モデルであることは言うまでもありません。 ここでは、（特に元のモデル）のすべての仮定が実際に経験的に有効であるわけではないことが強調されるべきである。, 例えば、重要な制限は次のとおりです。

• 株式の極端な動きの過小評価、テールリスクをもたらす
• インスタント、コストレス取引の仮定、流動性リスクをもたらす
• 定常プロセスの仮定、ボラティリティリスクをもたらす
• 継続的な時間と取引の仮定、ギャップリスクをもたらす

これらは、アウト-オブ-ザ-マネーでヘッジすることによって、任意およびすべての投資戦略において考慮されるべきである。オプション、複数の取引所での取引、ボラティリティヘッジとガンマヘッジとのヘッジ、それぞれ。,

背景

簡単に述べたように、fischer BlackとMyron Scholesは、1973年に、特定のルールに従ってポートフォリオを動的に改訂すると、基礎となるセキュリティの期待されるリターンが取り除かれることを示しました(Black&Scholes,1973)。 そのモデルが築いた作品Bachelier,サミュエルソンなど。 Robert C.Mertonは、このモデルの理解を拡大した論文を最初に発表し、”Black-Scholes options pricing model”という用語を造語した人物でした。, スコールズとマートンは、基礎となる有価証券のリスクからストックオプションを離婚する方法の発見により、1997年のノーベル経済科学賞を受賞しました。 1995年にフィッシャー-ブラックが亡くなったため、ノーベル賞を受賞する資格はなかったが、ノーベルアカデミーから寄稿者として認められた。