レッスンインデックスに戻る|順序でレッスンを行う|印刷に適したページ

有理根検定：はじめに（page1of2）

多項式のゼロは、ゼロの値を返す入力値（通常はx値）多項式にプラグインするときの多項式全体に対して。 ゼロが実数（つまり複素数ではない）のとき、それは多項式関数のグラフのx切片でもあります。, あなたは頻繁に（特に微積分学で）与えられた多項式関数のゼロの位置を知りたいと思うでしょう。 あなたは多項式に数字を差し込むことができ、行き当たりばったりで、最善を願っています。 しかし、あなたが二次式を勉強したときに学んだように、ゼロはしばしば非常に厄介な数字です。 それでは、どのようにゼロを見つけようとしていますか？有理根（または有理ゼロ）テストは、多項式のゼロ（根）を見つけようとしているときに有用な最初の推測のリストを取得する便利な方法です。, 整数（すなわち、正と負の”整数”）係数を持つ多項式が与えられたとき、可能な（または可能性のある）ゼロは、先行係数の因子に対する定数（最後の）項の因子をリストすることによって見つけられ、したがって分数のリストを形成する。 このリストは、テストする可能性のある有理数（分数）根のリストを提供します-したがって、テストの名前です。

強調してみましょう：有理根検定はあなたにゼロを与えません。 それは間違いなくゼロが何になるかを言っていません。, このテストでは、多項式で試すのが比較的簡単で”素敵な”数のリストしか与えられません。 これらの可能性のあるゼロのほとんどは、実際にはゼロではないことが判明します！

単純な多項式を見ることで、テストの方法論の感覚を見ることができます。 二次12×2-7x-10を考えると、二次式を使ってゼロを見つけることができますが、12×2–7x–10=（3x+2）（4x–5）を得るために因数分解することもできます。 ゼロに等しい二つの要因を設定すると、x=–2/3とx=5/4で二つの根が得られます。, 分母”3″および”4″は先行係数”12″の因子であり、分子”2″および”5″は定数項”10″の因子であることに注意してください。 すなわち、ゼロは、先行係数（10）の因子に対する定数項（12）の因子からなる分数である。 ただし、5/6や–10/3などの分数もこのように形成される可能性があります（したがって、テストによって提供されます）が、これらの他の分数は実際にはこの二次のゼロではないことに注意してください。,

この関係は常に真です：多項式が有理根を持つ場合、それらの根はフォームの分数（プラスまたはマイナス）（定数項の係数）/（主要係数の係数）になります。 しかし、この形式のすべての分数が必ずしも多項式のゼロであるわけではありません。 実際、そのように形成された分数のどれも実際には多項式のゼロではないことが起こるかもしれません。

そのようなルーツがある場合は、”潜在的な”ルーツ、”可能な”ゼロ”と言い続けることに注意してください。..”., これは、有理根検定によって生成された分数のリストが潜在的な解のリストに過ぎないためです。 分数のいずれかが実際に解であることは真実である必要はありません。 分数の根はないかもしれません！ たとえば、x2–2が与えられた場合、有理根検定は次の可能な有理ゼロを与えます。

しかし、あなたはすでにそれを知っています：

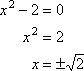
…したがって、ゼロは実際にはまったく有理ではありません。,

常に覚えておいてください：合理的なルーツテストは、良い最初の推測のリストを与えるだけです。

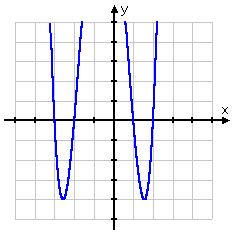
• x4+2×3-7×2–8x+12のすべての可能な有理x切片を見つけます。

Top | 1 | 2 | Return to Index Next >>