可換、結合および分配法則
うわー! どのような言葉の一口! しかし、アイデアは簡単です。
可換法則
“可換法則”は、数を交換しても同じ答えを得ることができると言います。..
。.. 追加するとき:
a+b=b+a
例:
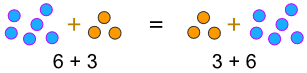
。.. または、乗算するとき:
a×b=b×a
例:
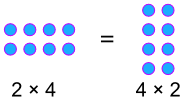
可換パーセンテージ!,
a×b=b×aなので、bの%=b%のa
例:8%の50=50%の8、つまり4

なぜ”可換”なのか。.. ?
数字は通勤者のように前後に移動することができるからです。
連想法則
“連想法則”は、数値をどのようにグループ化するか(つまり、最初に計算するか)は問題ではないと言います。..
。.., 追加するとき:
(a+b)+c=a+(b+c)
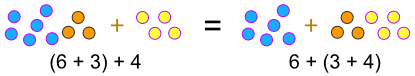
。..,td>
(2 + 4) + 5 = 6 + 5 = 11
| これは | (3 × 4) × 5 = 12 × 5 = 60 |
| はこれと同じ答えを持っています: | 3 × (4 × 5) = 3 × 20 = 60 |
使用します:
時にはそれは別の順序で追加または乗算する方が簡単です:
何ですか19 + 36 + 4?,
19 + 36 + 4 = 19 + (36 + 4)
=19+40=59
または少し再配置する:
2×16×5とは何ですか?
2 × 16 × 5 = (2 × 5) × 16
=10×16=160
分配法則
“分配法則”はすべての中で最高のものですが、細心の注意が必要です。,
これは私たちができることです:
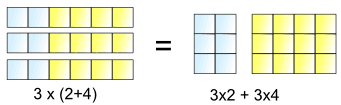
3lots of(2+4)は3lots of2plus3lots of4と同じです
したがって、3×は2+4全体で3×2と3×4に”分散”することができます。
a×(b+c)=a×b+A×c
自分で計算を試してみてください:
- 3 × (2 + 4) = 3 × 6 = 18 <李>3×2 + 3×4 = 6 + 12 = 18
どちらにしても同じ答えが得られます。,
英語で言うことができます:
私たちは同じ答えを得るとき:
- 一緒に追加された数字のグループで数を掛けるか、
- それぞれ別々に掛けてからそれらを追加します
用途:
難しい乗算を分割する方が簡単です:
例:6×204とは何ですか?
6 × 204 = 6×200 + 6×4
=1,200+24
=1,224
または組み合わせるには:
例:16×6+16×4とは何ですか?,
16 × 6 + 16 × 4 = 16 × (6+4)
=16×10
=160
減算でも使用できます。
例: 26×3 – 24×3
=2×3
=6
追加の長いリストにも使用できます。
例: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
=20×7
=140
。 . . しかし、あまりにも遠くに行くな!,
可換法則は減算または除算には機能しません。
例:
- 12/3=4ですが、
- 3/12=√
連想法則は減算または除算には機能しません。















