아주 비공식적으로는,두 개의 측면에서 합계에 의해 주어진 블랙-숄즈 공식될 수 있으로의 생각’의 현재 가격에 주식을 가중치로는 확률 운동을 것입니다 당신의 선택권을 구입하는 주식’마이너스’할인된 가격의 운동하는 옵션을 가중하여 확률이 당신이 선택권을 운동’, 또는 단순히’무엇을 얻을하고자하는’마이너스’당신은 당신이 지불'(칸,2013).,

유럽 옵션을 넣어(계약에 대해 권리,하지만 의무는,판매하는 몇 가지 밑에 깔 자산이 사전에 결정 가격이 미리 결정 날짜 이후)해당 기능적 형태:

예:을 계산하는 가격은 유럽의 전화 옵션

을 계산하기 위해 무엇을 가격은 유럽의 전화 옵션은,우리는 우리가 필요한 다섯가 필요한 값을 방정식 6 니다. 그들은:1. 주식(들)의 현재 가격,2. 콜 옵션의 행사 가격(엑스),3. 만료 시간(T-t),4. 무위험 이자율(r)과 5., 역사적 로그 수익률(σ)의 표준 편차에 의해 주어진 주식의 변동성.

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

우리는 우리를 추정할 수 있는 모든 주가의 변동성을 관찰하여 역사적인 가격,또는,더 간단히 계산하여 다른 옵션의 가격은 동일한 주식에서 다른 성숙/의 만료날짜(T)및 운동/strike 가격(X)만약 우리가 알고,그에 따라 설정 블랙-숄즈 모델입니다. 결과 값인 σ 는 0 에서 1 사이의 숫자로 주식에 대한 시장의 묵시적 변동성을 나타냅니다., 테슬라 대해 글을 쓰는 시점에서 본 문서의 가치 평균 약 0.38 4-5 다른 옵션 가격의 주변에는 동일 만기/성숙 날짜입니다. 위의 방정식 6 에 입력하면,우리가 관심있는 콜 옵션은$7 정도의 어딘가의 가격이어야한다는 것을 알 수 있습니다.

묵시적 변동성

지만 그것은 흥미로운 방법을 이해하는 옵션을 발행인에 도착하는 가격은 그들의 전화를 넣어 옵션,투자자로서 그것이 어렵다”동의”이와 같은 가격,per se,그리고 그렇게 어려운 이 지식으로 실행 가능한 투자라고 볼 수 있다.,

우리는 그러나 많이 얻는 사용량의 블랙-숄즈 공식하면 대신 우리는 치료의 가격이션(C 또는 P)으로 알려진 수량/독립변수(발견하여서 다른 성숙/만료 날짜 T 과 다른 운동 가격 X) 이 때문에,우리가 할 경우,블랙-숄즈 기능식 도구하는 방법을 이해하는 데 도움이되는 시장의 추정의 변동성을 주식으로도 알려져 있는 묵시적 변동성의 옵션입니다. 이것은 우리가 이상 동의하지 않을 수 있습니다 정보입니다,과에 대한 무역.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called “continuous timeline instruments”), they are much more difficult to deal with that European options (“point in time instruments”)., 주로 때문에,최적의 운동 정책 것의 가치에 영향을 미치는 옵션이 필요할 때 계정으로 수행을 해결하 블랙-숄즈 편미분 방정식이다. Black-Scholes 방정식에 따르면 미국 옵션에 대한 알려진”닫힌 형태”솔루션은 없습니다. 가 있지만,일부 특별한 경우:

• 에 대한 미국의 통화에서 옵션을 근본적인 자산을 지불하지 않 배당금(또는 기타 지급),미국의 통화 옵션 가격과 동일한 유럽 전화 옵션이 있습니다. 이 경우 최적의 운동 정책은 옵션을 행사하지 않기 때문입니다.,
• 에 대한 미국의 통화 옵션에 기초자산을 하나 알려진 배당의 수명에,그것은 최적의 수 있습니다 운동의 옵션을 조기에 종료하게 됩니다., 그러한 경우에 할 수있는 옵션을 최적으로 행사하기 전에 재고가 배당락에 따라 솔루션의 주에서 폐쇄 형태에 의하여 소위 Roll-Geske-웰 방법(롤,1977;Geske,1979;1981 년웰,1981):

첫 번째는지 확인하면 그것은 최적의 운동하는 옵션이 초기 조사하여 여부는 다음과 같은 불평등은 성취되:

S=주식 가격,X=운동 가격,D₁=배당금 지급,t=현재 날짜,t₁=날짜의 배당금을 지불,T=의 만료 날짜 옵션입니다.

불평등이 충족되지 않으면 조기에 최적이 아닌 운동을하십시오., 경 C(・)일반적인 블랙-숄즈에 대한 공식 유럽의 통화에서 옵션을 비 배당금 지불 주가(eq x)값이 미국화 옵션은 다음에 의해 주어진 버전의 동일한 방정식이 어디 주식 가격(S)가 할인:

경우에는 불평등이 달성된 후에는 초기 운동은 최적의의 값은 미국의 통화 옵션에 의해 주어진 다음,끔찍한,의 혼란 방정식(I 스도를 믿으로 각 용어를 더 읽기 가능):

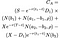
어디로 전 S=주식의 가격,T=일의 만료 옵션,X=운동 가격 및 r=위험 관심을 평가,σ=변동성(표준 편차 로그의 역사의 주식)및 D₁ 은 배당금을 지급. 또한,ρ 에 의해 제공됩니다.

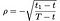
a₁, a₂ by:

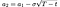
and b₁, b₂ by:

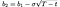
제한 사항

말 없이는 블랙-숄즈 모델을 정확하게하는,이론적 모델을 시도하는 견적하는 방법 시장 동작하는 주어진 가정을 위에 설명한 고유한 제한을 우리 자신의 숫자 추정 위험의 이자율(r)그리고 미래 변동성(σ). 여기서(특히 원래 모델)의 모든 가정이 실제로 경험적으로 유효하지는 않다는 점을 강조해야합니다., 예를 들어,중요한 제한 사항이 발생 from:

• 의 과소 평가 극단적인 움직임에서 주식을 산출,꼬리 위험
• 의 가정은 즉시 비용이 덜 무역을 산출,유동성 위험
• 가정의 고정식 프로세스,수익 변동성 위험
• 가정의 지속적인 시간 및 거래 항복 격차를 위험

이러한 차지한에서는 모든 투자 전략에 대한 인스턴스를 통해 위험 회피와 나의 돈,옵션 거래에 여러 교류,헤징과 변동성을 회피 및 감마 헤지,각각합니다.,

배

으로 간단하게 그것을 언급했 Fischer 까만 및 마이런 Scholes 는 1973 년여 동적으로 수정 포트폴리오를 일정한 규칙에 따라 제거한 것으로 예상 수익의 기본 보안(블랙&Scholes,1973). 그들의 모델은 Bachelier,Samuelson 및 다른 사람들이 이전에 설립 한 작품을 기반으로했습니다. 로버트 C. 머하는 첫번째이었다 게시하는지 확장에 대한 이해의 모델은 누가 만들어낸 용어”블랙-숄즈 옵션 가격 모델”., Scholes 와 머을 수상했 1997 년 노벨 기념상에서 경제학에 대한 그들의 검색 방법의 이혼식 옵션에서 위험의 근본적인 증권. 피셔 블랙이 1995 년에 세상을 떠났을 때,그는 상을받을 자격이 없지만 노벨 아카데미의 기고가로 인정 받았다.피>