로 돌아가 수업을 인덱스|할 수업에서 주문|인쇄 페이지

합리적인 뿌리 테스트 소개(1/2 페이지)

으로 다항식의 입력 값(일반적으로 x-값)을 반환하는 값의 전체에 대한 다항식 때 당신은 플러그인으로 그것을 다항식. 0 이 실제(즉,복잡하지 않은)숫자 일 때 다항식 함수의 그래프의 x 절편이기도합니다., 당신은 자주(특히 미적분학에서)주어진 다항식 함수의 0 의 위치를 알고 싶어 할 것입니다. 다항식에 숫자를 꽂고 다짜고짜 다짜고짜 다짜고짜 다짜고짜 다짜고짜 다짜고짜 다짜고짜 다짜고짜 다짜고짜 다짜고짜 그러나 당신이 배운 것을 때 당신이 공부하 차 수식,제로는 종종 매우 지저분한 숫자 임의로 추측은 아마 최고의 계획을 공격합니다. 그래서 어떻게 하나는 0 을 찾으려고 노력에 대해 이동합니까?

리 뿌리(또는 합리적인 제로)테스트는 편리한 방법이 유용한의 목록을 먼저 추측을 때 당신은 당신을 찾으려고 노력 제로(뿌리)의 다항식., 주어진 다항식과 정수(즉,긍정적이고 부정적인”전체 수”)계수를 가능한(또는 잠재적)규에 의해 발견 목록 요인의 일정(마)기간을 통해 요소의 선도 계수,이렇게 형성하는 목록의 하나입니다. 이 목록은 테스트 할 잠재적 인 합리적인(분수)루트 목록을 제공합니다.

강조하겠습니다:합리적인 뿌리 테스트는 당신에게 0 을주지 않습니다. 그것은 0 이 확실히 될 것이라고 말하지 않습니다., 이 테스트는 다항식에서 시도 할 수있는 비교적 쉽고”좋은”숫자 목록 만 제공합니다. 이러한 가능한 0 의 대부분은 실제로 0 이 아닌 것으로 판명 될 것입니다!

간단한 다항식을 보면 테스트의 방법론에 대한 감각을 알 수 있습니다. 2 차 12×2-7x-10 이 주어지면 2 차 공식을 사용하여 0 을 찾을 수 있지만 12×2–7x–10=(3x+2)(4x–5)를 얻기 위해 계수를 지정할 수도 있습니다. 두 요인을 0 과 동일하게 설정하면 x=–2/3 및 x=5/4 에서 두 개의 뿌리를 얻습니다., 분모”3″과”4″는 선행 계수”12″의 요인이고 분자”2″와”5″는 상수 용어”10″의 요인이라는 점에 유의하십시오. 즉,0 은 선행 계수(12)의 요인에 대한 상수 항(10)의 요인으로 형성된 분수입니다. 참고 또한,그러나,분수와 같은 5/6 및 10/3 수도 있습 형성된 이 방법으로(따라서 제공한 테스트),그러나 이러한 다른 분수하지 않은 사실이 영의 차입니다.,

이 관계는 항상 진실하는 경우 다항식은 합리적 뿌리,그 뿌리는 것입니다 분수의 양식을(플러스 마이너스)(인자의 일정한 기간)/(요소의 선도 계수). 그러나이 형태의 모든 분수가 반드시 다항식의 0 이되는 것은 아닙니다. 실제로,그렇게 형성된 분수 중 어느 것도 실제로 다항식의 0 이 아니라는 것이 발생할 수 있습니다.

참고하는 내가 계속 말하는”잠재적인”뿌리”가능한”제로,”이 있는 경우 이러한 뿌리입니다…”., 이것은 합리적인 뿌리 테스트에 의해 생성 된 분수 목록이 잠재적 인 해결책의 목록 일 뿐이기 때문입니다. 분수 중 하나가 실제로 해결책이라는 것은 사실 일 필요는 없습니다. 분수 뿌리가 없을 수도 있습니다! 예를 들어,주어진 x2–2,합리적 뿌리 시험은 다음과 같은 가능한 합리적인 제로.

하지만 당신은 이미 알고 있:

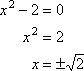
…그래서를 제로지 않은 실제로 합리적이다.,

항상 기억하십시오:합리적인 뿌리 테스트는 좋은 첫 번째 추측 목록 만 제공합니다.

• x4+2×3-7×2-8x+12 의 가능한 모든 합리적인 x-인터셉트를 찾으십시오.

Top | 1 | 2 | Return to Index Next >>