정류,연관 및 분배 법칙
와우! 이 얼마나 한 입의 단어! 그러나 아이디어는 간단합니다.
정류 법칙
“정류 법칙”은 우리가 숫자를 바꿔서 여전히 같은 대답을 얻을 수 있다고 말합니다…<피>… 우리가 추가 할 때:
a+b=b+a
예:
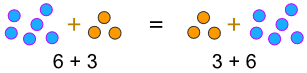
… 나 때 우리는 곱:
a x b=b×
예:
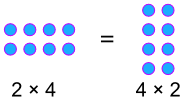
환율!,
a×b=b×a 의 a%가 a
예:4

왜”commutative”… ?숫자가 통근자처럼 앞뒤로 여행 할 수 있기 때문입니다.
연관 법
“연관 법률”말든 문제가 되지 않는다는 것을 어떻게 우리가 그룹 숫자(즉,우리가 계산을 먼저)…<피>…, 우리가 추가 할 때:
(a+b)+c=a+(b+c)
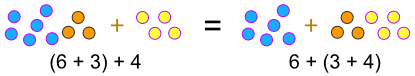
…,r>
| 이다: | (3 × 4) × 5 = 12 × 5 = 60 |
| 같은 응답이: | 3 × (4 × 5) = 3 × 20 = 60 |
사용:
때로는 보다 쉽게 추가 또는 곱 다른 순서:
은 무엇인 19 + 36 + 4?,
<피>19 + 36 + 4 = 19 + (36 + 4)
=19+40=59
또는 조금 다시 정렬하려면
2×16×5 는 무엇입니까?
<피>2 × 16 × 5 = (2 × 5) × 16 배 법칙이 가장 좋지만 세심한주의가 필요합니다.,
이것은 우리에게
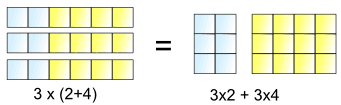
3 의(2+4)동일 3 개의 2 및 3 의 많은 4
그리고,3×이 될 수 있습니다”분산된”2+4, 3×2,3×4
And we write it like this:
×(b+c)=a x b+a×c
도 계산을 직접:
- 3 × (2 + 4) = 3 × 6 = 18
- 3×2 + 3×4 = 6 + 12 = 18
방법 중 하나로 같은 대답합니다.,
영어로 우리가 말할 수 있습니다:
우리는 같은 대답을 얻을 때 우리는다.
- 곱 숫자의 그룹에 의해 번호를 추가 함께,또는
- 각 곱 별도로 그들을 추가
사용:
때때로 그것이 쉽게 나누기 어려운 곱하기:
예:는 무엇입 6×204?
<피>6 × 204 = 6×200 + 6×4
=1,200+24
=1,224
또는 결합:
예:16×6+16×4 란 무엇입니까?,
16 × 6 + 16 × 4 = 16 × (6+4)
=16×10
=160
우리는 그것을 이용할 수 있습에서 빼기를 너무
예: 26×3 – 24×3
=2×3
=6
우리는 우리가 그것을 사용할 수 있습니한의 긴 목록을 추가,도:
예: 6×7 + 2×7 + 3×7 + 5×7 + 4×7
6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
=20×7
=140
. . . 그러나 너무 멀리 가지 마라!,
교환법이 작동하지 않거나 빼기위한 부:
예:
- 12/3=4,하지만
- 3/12=¼
연관 법률이 작동하지 않거나 빼기위한 부:















