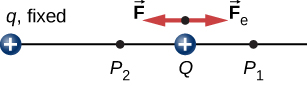
Quando um livre de carga positiva q é acelerado por um campo elétrico, é dada energia cinética (Figura \(\PageIndex{1}\))., O processo é análogo a um objeto que está sendo acelerado por um campo gravitacional, como se a carga estivesse descendo uma colina elétrica onde sua energia potencial elétrica é convertida em energia cinética, embora, naturalmente, as fontes das forças sejam muito diferentes. Vamos explorar o trabalho feito sobre uma carga q pelo campo elétrico neste processo, para que possamos desenvolver uma definição de energia potencial elétrica.

a força eletrostática ou Coulomb é conservadora, o que significa que o trabalho feito em q é independente do caminho tomado, como demonstraremos mais tarde., Isto é exatamente análogo à força gravitacional. Quando uma força é conservadora, é possível definir uma energia potencial associada à força. Normalmente é mais fácil trabalhar com a energia potencial (porque depende apenas da posição) do que calcular o trabalho diretamente.

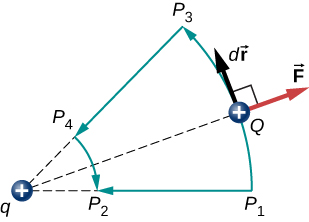
O trabalho \(W_{12}\) realizado pela força aplicada \(\vec{F}\) quando a partícula se move de \(P_1\) para \(P_2\) pode ser calculado por

\

\

, onde temos definida positiva para estar apontando para longe da origem, e r é a distância da origem. As direções do deslocamento e da força aplicada no sistema na figura \(\PageIndex{2}\) são paralelas, e assim o trabalho feito no sistema é positivo.

usamos a letra U para designar a energia potencial elétrica, que tem unidades de joules (J)., Quando uma força conservadora faz um trabalho negativo, o sistema ganha energia potencial. Quando uma força conservadora faz um trabalho positivo, o sistema perde energia potencial, \(\Delta U = – W\). No sistema da figura \(\PageIndex{3}\), a força de Coulomb age na direção oposta ao deslocamento; portanto, o trabalho é negativo. No entanto, aumentámos a energia potencial no sistema de duas cargas.

neste exemplo, o trabalho feito para acelerar uma carga positiva do descanso é positivo e resulta de uma perda em U, ou um negativo \(\Delta U\)., Um valor para U pode ser encontrado em qualquer ponto tomando um ponto como referência e calculando o trabalho necessário para mover uma carga para o outro ponto.a energia potencial gravitacional e a energia potencial elétrica são bastante análogas. A energia potencial é responsável pelo trabalho feito por uma força conservadora e dá uma visão adicional sobre a energia e a transformação da energia sem a necessidade de lidar diretamente com a força. É muito mais comum, por exemplo, usar o conceito de energia potencial elétrica do que lidar com a força de Coulomb diretamente em aplicações do mundo real.,

\

Note que Q é uma constante.

outra implicação é que podemos definir uma energia potencial elétrica. Lembre-se que o trabalho feito por uma força conservadora também se expressa como a diferença na energia potencial correspondente a essa força., Por isso, o trabalho \(W_{ref}\) para levar uma carga de um ponto de referência para um ponto de interesse pode ser escrito como

\

e, pela Equação \ref{7.1}, a diferença de energia potencial (\(U_2 – U_1\)) do teste de carga Q entre os dois pontos

\

Portanto, podemos escrever uma expressão geral para a energia potencial de duas cargas puntiformes (em coordenadas esféricas):

\_{r_{ref}}^r = kqQ\à esquerda.,\]

Podemos tomar o segundo termo a ser uma constante arbitrária nível de referência, que serve como referência zero:

\

Uma escolha conveniente de referência que depende de nosso senso comum é de que quando as duas cargas são infinitamente distantes, não há interação entre eles. (Recordar a discussão da energia potencial de referência em energia potencial e conservação de energia., A ) tendo o potencial de energia do estado de zero remove o termo \(U_{ref}\) a partir da equação (assim como quando dizemos que a terra é zero de energia potencial em energia potencial gravitacional problema), e a energia potencial do Q quando ela é separada do q a uma distância r, assume a forma

\

Devido a lei de Coulomb, a força devido a vários encargos sobre uma carga de prova \(P\) sobrepor; eles podem ser calculados individualmente e, em seguida, acrescentou. Isto implica que as integrais de trabalho e, portanto, as energias potenciais resultantes exibem o mesmo comportamento., Para demonstrar isso, consideramos um exemplo de montar um sistema de quatro taxas.

Note que o potencial elétrico de energia é positivo se as duas cargas são de mesmo tipo, positivo ou negativo, e o negativo se os dois encargos são de tipos opostos. Isto faz sentido se você pensar na mudança na energia potencial \(\Delta U\) à medida que você aproximar as duas cargas ou movê-las mais longe., Dependendo dos tipos relativos de Taxas, você pode ter que trabalhar no sistema ou o sistema iria trabalhar em você, ou seja, seu trabalho é positivo ou negativo. Se você tem que fazer um trabalho positivo no sistema (na verdade, empurrar as cargas mais perto), então a energia do sistema deve aumentar. Se você aproximar duas cargas positivas ou duas cargas negativas, você tem que fazer um trabalho positivo no sistema, o que aumenta sua energia potencial. Uma vez que a energia potencial é proporcional a 1/r, a energia potencial sobe quando r desce entre duas cargas positivas ou duas negativas.,

Por outro lado, se você trazer uma carga positiva e negativa mais perto, você tem que fazer um trabalho negativo no sistema (as cargas estão puxando você), o que significa que você tira energia do sistema. Isto reduz a energia potencial. Uma vez que a energia potencial é negativa no caso de um par de cargas positivas e negativas, o aumento em 1/r torna a energia potencial mais negativa, o que é o mesmo que uma redução na energia potencial.

O resultado do exemplo \(\PageIndex{2}\) pode ser estendido A SISTEMAS com qualquer número arbitrário de encargos., Neste caso, é mais conveniente escrever a fórmula como

\

o Fator de 1/2 conta para adicionar cada par de cargas duas vezes.