Muito informalmente, os dois termos na soma dada por Black-Scholes fórmula pode ser pensado como ‘o preço atual das ações ponderadas pela probabilidade de que você vai exercer a sua opção para comprar o estoque’ menos ‘o desconto de preço de exercício da opção, ponderada pela probabilidade de que você irá exercer a opção’, ou, simplesmente, “o que você está indo para obter’ menos ‘o que você está indo para pagar” (Khan, 2013).,

Para um Europeu de opção de venda (contratos para o direito, mas não obrigação, de vender alguns underlaying ativo a um preço pré-determinado em uma pré-determinada data no futuro) o equivalente funcional do formulário:

Exemplo: Calcular o preço de uma opção Européia de compra

para calcular o preço de uma opção Européia de compra deve ser, sabemos que temos cinco valores exigidos pela equação 6 acima. Eles são: 1. O preço atual das ações, 2. O preço de exercício da opção call (X), 3. O tempo de expiração (T-t), 4. A taxa de juro sem risco (r) e 5., A volatilidade do stock, dada pelo desvio-padrão dos registos históricos (σ).

podemos estimar a volatilidade de qualquer estoque observando seus preços históricos, ou, ainda mais simples, calculando outros preços de opção para o mesmo estoque em diferentes prazos de vencimento/expiração (T) e preços de exercício / greve (X), se soubermos que eles foram definidos de acordo com um modelo Black-Scholes. O valor resultante, σ, é um número entre 0 e 1, representando a volatilidade implícita do mercado para o estoque., Para a Tesla, no momento da redacção deste artigo, o valor médio era de aproximadamente 0,38 para 4-5 diferentes preços das opções em torno da mesma data de expiração/maturidade. Entrada na equação 6 acima, achamos que a opção de chamada em que estamos interessados deve ser Preços em torno de US $7.

volatilidade Implícita

Embora seja interessante para entender como opções de emitentes chegar ao preço de suas opções call e put, como investidores é difícil “discordo” com esses preços, por si só, e tão difícil para tornar esse conhecimento acionável investimento teses.,

no entanto, podemos ter um monte de kilometros de Black-Scholes fórmula se nós em vez de tratar o preço de uma opção (C ou P) como uma quantidade conhecida/variável independente (encontrados em diferentes vencimento/datas de vencimento T e diferentes preços de exercício X). Isto porque, se o fizermos, a equação funcional Black-Scholes torna-se uma ferramenta para nos ajudar a entender como o mercado estima a volatilidade de um estoque, também conhecido como a volatilidade implícita da opção. Esta é uma informação que podemos discordar e negociar contra.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called “continuous timeline instruments”), they are much more difficult to deal with that European options (“point in time instruments”)., Principalmente, uma vez que a Política de exercício ideal afetará o valor da opção, isso precisa ser levado em conta ao resolver a equação diferencial parcial Black-Scholes. Não existem soluções conhecidas de “forma fechada” para as opções americanas de acordo com a equação de Black-Scholes. Existem, no entanto, alguns casos especiais:

• Para As opções de compra americanas sobre activos subjacentes que não pagam dividendos (ou outros pagamentos), o preço da opção de compra Americana é o mesmo que para as opções de compra Europeias. Isto porque a Política de exercício ideal neste caso é não exercer a opção.,para as opções de compra americanas sobre activos subjacentes que pagam um dividendo conhecido ao longo da sua vida, pode ser óptimo exercer a opção mais cedo., Em tais casos, a opção pode ser perfeitamente exercida apenas antes que o estoque vai de ex-dividendo, de acordo com uma solução em forma fechada pelo chamado Roll-Geske-Whaley (método de Rolo, 1977; Geske, 1979; 1981; Whaley, 1981):

Primeiro, verifique se ele é o ideal para o exercício da opção de início, investigando se a seguinte desigualdade é satisfeita:

Para S = preço da ação, X = preço de exercício, D₁ = dividendo pago, t = data atual, t₁ = a data de pagamento de dividendos, T = data de expiração da opção.

Se a desigualdade não for cumprida, o exercício precoce não é o ideal., Se C(・) é normal Black-Scholes fórmula para opções de compra Européia sobre a não-dividendos-pagamento de estoque (eq x), o valor da opção Americana de compra, em seguida, é dada por uma versão da mesma equação, onde o preço das ações da (S) está com desconto:

Se a desigualdade é cumprida, início de exercício é ótimo e o valor da opção Americana de compra é dado pela seguinte, terrível, bagunça de uma equação (eu tentei quebrá-lo, por cada prazo para torná-lo mais legível):

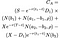
Onde, como antes, que S = preço da ação, T = data do vencimento da opção, X = preço de exercício e r = taxa de juro sem risco, σ = volatilidade (desvio padrão de log de histórico de retornos das ações), e D₁ é o dividendo. Além disso, ρ é dada por:

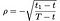
a₁, a₂ by:

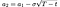
and b₁, b₂ by:

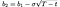
Limitações

Ele deve ir sem dizer que Black-Scholes o modelo é exatamente isso, um modelo teórico que tenta estimar como um mercado se comporta, dadas as suposições acima referido e as limitações inerentes a nossa própria numérica estimativas de livre de risco de taxas de juros (r) e o futuro volatilidade (σ). É de salientar que nem todos os pressupostos (especialmente o modelo original) são, de facto, empiricamente válidos., Por exemplo, limitações significativas surgir a partir de:

• A subestimação de extrema move-se em ações, produzindo cauda risco
• O pressuposto de imediato, o custo-menos de negociação, gerando risco de liquidez
• O pressuposto de um processo estacionário, gerando o risco de volatilidade
• A suposição de tempo contínuo e de negociação, produzindo lacuna risco

Estes devem ser contabilizados em qualquer e todas as estratégias de investimento, por exemplo, a cobertura com out-of-the-money opções de negociação em vários intercâmbios, cobertura com a volatilidade da cobertura e da Gama de cobertura, respectivamente.,

Fundo

Como mencionado brevemente era Fischer Black e Myron Scholes, que, em 1973, mostrou que dinamicamente a revisão de uma carteira de acordo com certas regras remove o retorno esperado do ativo subjacente (Preto & Scholes, 1973). Seu modelo foi construído em obras anteriormente estabelecidas por Bachelier, Samuelson e outros. Robert C. Merton foi o primeiro a publicar um artigo expandindo a compreensão do modelo e que cunhou o termo “Black-Scholes options pricing model”., Scholes and Merton was awarded the 1997 Nobel Memorial Prize in Economic Sciences for their discovery of the method of divorcing stock options from the risk of their underlying securities. Como Fischer Black Faleceu em 1995, ele não seria elegível para receber o prêmio, mas foi reconhecido como um Contribuinte pela Academia Nobel.