den elektrostatiska eller Coulomb-kraften är konservativ, vilket innebär att arbetet på q är oberoende av den väg som tagits, som vi kommer att visa senare., Detta är exakt analogt med gravitationskraften. När en kraft är konservativ är det möjligt att definiera en potentiell energi i samband med kraften. Det är vanligtvis lättare att arbeta med den potentiella energin (eftersom det bara beror på position) än att beräkna arbetet direkt.

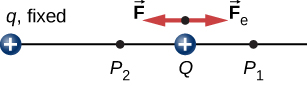
arbetet \(W_{12}\) gjort av den applicerade kraften \(\vec{f}\) när partikeln rör sig från \(P_1\) till \(p_2\) kan beräknas med

\

\

\

där vi har definierat positivt att peka bort från ursprunget och r är avståndet från ursprunget. Riktningarna för både förskjutningen och den applicerade kraften i systemet i Figur \(\PageIndex{2}\) är parallella, och därmed är arbetet på systemet positivt.

vi använder bokstaven U för att beteckna elektrisk potentiell energi, som har enheter av joule (J)., När en konservativ kraft gör negativt arbete, får systemet potentiell energi. När en konservativ kraft gör positivt arbete förlorar systemet potentiell energi, \(\Delta U = – W\). I systemet i Figur \(\PageIndex{3}\) verkar Coulomb-kraften i motsatt riktning mot förskjutningen; därför är arbetet negativt. Vi har dock ökat den potentiella energin i tvåladdningssystemet.

i det här exemplet är arbetet med att påskynda en positiv laddning från Vila positivt och beror på en förlust i U eller en negativ \(\Delta U\)., Ett värde för U kan hittas när som helst genom att ta en punkt som referens och beräkna det arbete som behövs för att flytta en avgift till den andra punkten.

gravitationspotential energi och elektrisk potentiell energi är ganska analoga. Potentiell energi står för arbete som utförs av en konservativ kraft och ger ökad insikt om energi-och energiomvandling utan att det är nödvändigt att hantera kraften direkt. Det är mycket vanligare att till exempel använda begreppet elektrisk potentiell energi än att hantera Coulomb-kraften direkt i verkliga tillämpningar.,

\

Observera att Q är en konstant.

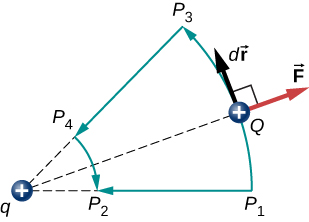
en annan implikation är att vi kan definiera en elektrisk potentiell energi. Minns att arbetet med en konservativ kraft också uttrycks som skillnaden i den potentiella energi som motsvarar den kraften., Därför kan arbetet \(W_{ref}\) för att få en laddning från en referenspunkt till en intressepunkt skrivas som

\

och, genom ekvation \ref{7.1}, skillnaden i potentiell energi (\(u_2 – U_1\)) av testladdningen Q mellan de två punkterna är

\

därför kan vi skriva ett allmänt uttryck för den potentiella energin hos två punktavgifter (i sfäriska koordinater):

\_{r_{Ref}}^r = KQQ\vänster.,\]

vi kan ta den andra termen för att vara en godtycklig konstant referensnivå, som fungerar som nollreferens:

\

ett bekvämt val av referens som bygger på vårt sunda förnuft är att när de två avgifterna är oändligt långt ifrån varandra finns det ingen interaktion mellan dem. (Minns diskussionen om referenspotential energi i potentiell energi och bevarande av energi., Att ta den potentiella energin i detta tillstånd till noll tar bort termen \(U_{ref}\) från ekvationen (precis som när vi säger att marken är nollpotential energi i ett gravitationspotential energiproblem), och den potentiella energin hos Q när den är skild från q med ett avstånd r antar formen

\

på grund av Coulombs lag, krafterna på grund av flera laddningar på en testladdning \(Q\) överlagras; de kan beräknas individuellt och sedan läggas till. Detta innebär att arbetsintegrationerna och därmed de resulterande potentiella energierna uppvisar samma beteende., För att visa detta anser vi ett exempel på att montera ett system med fyra laddningar.

Observera att den elektriska potentiella energin är positiv om de två laddningarna är av samma typ, antingen positiva eller negativa, och negativa om de två laddningarna är av motsatta typer. Detta är vettigt om du tänker på förändringen i den potentiella energin \(\Delta U\) när du tar de två laddningarna närmare eller flyttar dem längre ifrån varandra., Beroende på de relativa typerna av avgifter kan du behöva arbeta på systemet eller systemet skulle fungera på dig, det vill säga ditt arbete är antingen positivt eller negativt. Om du måste göra positivt arbete på systemet (faktiskt driva avgifterna närmare), bör systemets energi öka. Om du tar två positiva laddningar eller två negativa laddningar närmare, måste du göra positivt arbete på systemet, vilket ökar deras potentiella energi. Eftersom potentiell energi är proportionell mot 1 / r, går den potentiella energin upp när r går ner mellan två positiva eller två negativa laddningar.,

å andra sidan, om du tar en positiv och en negativ laddning närmare, måste du göra negativt arbete på systemet (avgifterna drar dig), vilket innebär att du tar energi bort från systemet. Detta minskar den potentiella energin. Eftersom potentiell energi är negativ i fallet med ett positivt och ett negativt laddningspar gör ökningen i 1 / r den potentiella energin mer negativ, vilket är detsamma som en minskning av potentiell energi.

resultatet från Exempel \(\PageIndex{2}\) kan utökas till system med valfritt antal avgifter., I det här fallet är det mest lämpligt att skriva formeln som

\

faktorn för 1/2 konton för att lägga till varje par avgifter två gånger.