mycket informellt, de två termerna i summan som ges av Black-Scholes-formeln kan ses som ”det nuvarande priset på beståndet viktat av sannolikheten att du kommer att utöva din möjlighet att köpa beståndet ”minus” det diskonterade priset för att utöva alternativet viktat av sannolikheten att du kommer att utöva alternativet”, eller helt enkelt ”vad du kommer att få ”minus” vad du ska betala ” (Khan, 2013).,

för en europeisk säljoption (kontrakt för rätten, men inte skyldighet, att sälja en del underliggande tillgång till ett förutbestämt pris på ett förutbestämt datum i framtiden) är den likvärdiga funktionella formen:

exempel: beräkna priset på en europeisk köpoption

för att beräkna vad priset på en europeisk köpoption ska vara, vi vet att vi behöver fem värden som krävs enligt ekvation 6 ovan. De är: 1. Det nuvarande priset på lager, 2. Övningspriset för samtalsalternativet (X), 3. Tiden till utgången (T – T), 4. Den riskfria räntan (r) och 5., Beståndets volatilitet, givet av standardavvikelsen för historiska loggreturer (σ).

Estimating the value of a call option for Tesla (TSLA)
The first four values we need are easily obtainable. Let’s say we are interested in a call option for Tesla’s stock ($TSLA), maturing the day of its Q3 earnings in 2019, at a price 20% higher than the stock is currently trading. Looking at Tesla’s NASDAQ listing ($TSLA) on Yahoo Finance today (July 13th, 2019), we find a stock price of S = $245. Multiplying the current price with 1.2 gives us an exercise price 20% higher than the stock is currently trading, X = $294. Googling, we find that the day of its Q3 earnings call is October 22nd, giving us a time to expiration/maturity of Oct 22nd - July 13th = 101 days. As a proxy for a risk-free interest rate instrument, we’ll use US 10-year government bonds ($USGG10YR), currently paying off 2.12%.So, we find S = 245, X = 294, T - t = 101 and r = 0.0212. The only missing value is an estimation of the stock’s volatility (σ).

Vi kan uppskatta alla lager volatilitet genom att observera dess historiska priser, eller, ännu enklare, genom att beräkna andra optionspriser för samma lager vid olika löptid/utgångsdatum (T) och motion / strike priser (X), om vi vet att de har ställts in enligt EN Black-Scholes modell. Det resulterande värdet, σ, är ett tal mellan 0 och 1, som representerar marknadens implicita volatilitet för beståndet., För Tesla, vid skrivandet av den här artikeln, var värdet i genomsnitt cirka 0,38 för 4-5 olika optionspriser runt samma utgångsdatum / förfallodag. Inmatning i ekvation 6 ovan finner vi att samtalsalternativet vi är intresserade av borde vara priser någonstans runt $ 7.

implicit volatilitet

även om det är intressant att förstå hur optionsemittenter kommer fram till priset på deras samtal och säljoptioner, eftersom investerare är det svårt att ”inte hålla med” med sådana priser, i sig, och så svårt att vända denna kunskap till åtgärds investeringsavhandlingar.,

Vi kan dock få mycket milage ur Black-Scholes-formeln om vi istället behandlar priset på ett alternativ (C eller P) som en känd kvantitet/oberoende variabel (hittades genom att titta på olika mognad/utgångsdatum T och olika övningspriser X). Detta för att om vi gör det blir den svarta-Scholes funktionella ekvationen ett verktyg för att hjälpa oss att förstå hur marknaden uppskattar volatiliteten hos ett lager, även känt som optionens implicita volatilitet. Detta är information som vi kan vara oense om, och handel mot.,

Hypothetical scenario
If we for instance look at the chart for the Tesla stock over the last three months (figure 2), we see a rather (for a lack of a better word) volatile journey from hovering around $280 three months ago, to a low of $180 a month and a half ago, to now on its way back up at $245. This makes sense given the volatility we observed from call prices before ($280–$180 = $100, $100/280 = 0.36, vs 0.38). It does not make sense, however, if we think the fluctuation over the past three months was the mere tip of an iceberg, going into a period of more volatility for Tesla, say, due to an upcoming increase in short-selling.

Let's say we disagree with an options issuer about the implied volatility of stock's performance over the last three months. We think the ride is going to get rockier. How much? Let's say that instead of 40%, we think the next three months will look more like 60%. Input into the functional Black-Scholes formula along with the same values for S, X, r, and T - t, we get a price of nearly twice of what the options issuer wants, at C(S,t) = $14.32. This we can trade on. We could, for instance, buy call options today and wait for volatility to increase or the value of the stock to go up, before selling at a profit.

American options

Because American options can be exercised at any date prior to expiration (so-called ”continuous timeline instruments”), they are much more difficult to deal with that European options (”point in time instruments”)., I första hand, eftersom den optimala träningspolicyn kommer att påverka värdet av alternativet, måste detta beaktas när man löser Black-Scholes partiella differentialekvation. Det finns inga kända ”slutna form” lösningar för amerikanska alternativ enligt Black-Scholes ekvation. Det finns dock vissa specialfall:

• för amerikanska samtalsalternativ på underliggande tillgångar som inte betalar utdelning (eller andra utbetalningar) är det amerikanska samtalsalternativet samma som För Europeiska samtalsalternativ. Detta eftersom den optimala träningspolicyn i detta fall är att inte utöva alternativet.,
• för amerikanska samtalsalternativ på underliggande tillgångar som betalar en känd utdelning under sin livstid kan det vara optimalt att utnyttja alternativet tidigt., I sådana fall kan alternativet utnyttjas optimalt strax innan beståndet går fritt utdelning, enligt en lösning som ges i sluten form av den så kallade Roll-Geske-Whaley-metoden (Roll, 1977; Geske, 1979; 1981; Whaley, 1981):

kontrollera först om det är optimalt att utöva alternativet tidigt genom att undersöka om följande ojämlikhet är uppfyllt:

För s = aktiekurs, X = övningspris, D = utdelning betald, t = aktuellt datum, t = utdelningsdatum, t = optionstidpunkt.

om ojämlikheten inte uppfylls, tidig övning det inte optimalt., Om C (-) är den vanliga Black-Scholes-formeln för Europeiska samtalsalternativ på icke-utdelningsbetalande lager (eq x), ges värdet av det amerikanska samtalsalternativet sedan av en version av samma ekvation där aktiekursen (arna) diskonteras:

om ojämlikheten är uppfylld är tidig träning optimal och värdet av det amerikanska samtalsalternativet ges av följande, hemska, röra av en ekvation (jag försökte bryta upp det med varje term för att göra det mer läsbart):

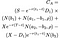
där som tidigare s = aktiekurs, t = Datum för optionens utgång, X = övningspris och r = riskfri ränta, σ = volatilitet (standardavvikelse för stockens historiska avkastning) och D är utdelningen. Dessutom ges ρ av:

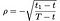
a₁, a₂ by:

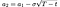
and b₁, b₂ by:

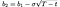
begränsningar

det borde vara självklart att Black-Scholes-modellen är just det, en teoretisk modell som försöker uppskatta hur en marknad beter sig, med tanke på de antaganden som anges ovan och de inneboende begränsningarna i våra egna numeriska uppskattningar av riskfria räntor (r) och framtida volatilitet (σ). Det bör här framhållas att inte alla antaganden om (särskilt den ursprungliga modellen) faktiskt är empiriskt giltiga., Till exempel uppstår betydande begränsningar från:

• underskattningen av extrema rörelser i beståndet, vilket ger svans risk
• antagandet om omedelbar, kostnadslös handel, vilket ger likviditetsrisk
• antagandet om en stationär process, vilket ger volatilitetsrisk
• antagandet om kontinuerlig tid och handel, vilket ger gaprisk

dessa bör redovisas i alla investeringsstrategier, till exempel genom säkring med out-of-the-penningoptioner, handel på flera börser, säkring med volatilitetssäkring respektive gammasäkring.,

Bakgrund

som kortfattat nämnde var det Fischer Black och Myron Scholes som 1973 visade att dynamiskt revidera en portfölj enligt vissa regler tar bort den förväntade avkastningen av den underliggande säkerheten (Svart& Scholes, 1973). Deras modell bygger på tidigare etablerade verk av Bachelier, Samuelson och andra. Robert C. Merton var den första som publicerade ett papper som utvidgade förståelsen för modellen och som myntade termen ”Black-Scholes options pricing model”., Scholes och Merton tilldelades 1997 Nobels Minnespris i Ekonomivetenskap för deras upptäckt av metoden att skilja aktieoptioner från risken för deras underliggande värdepapper. När Fischer Black gick bort 1995 skulle han inte vara berättigad att få priset, men erkändes som bidragsgivare av Nobelakademin.