Articles

Commutative, associativa och distributiva lagar

by admin

Wow! Vilken Munfull ord! Men idéerna är enkla.

kommutativa lagar

”kommutativa lagar” säger att vi kan byta nummer över och fortfarande få samma svar …

… när vi lägger till:

a + b = b + a

exempel:

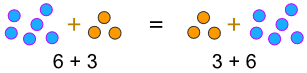
… eller när vi multiplicerar:

a × b = b × a

exempel:

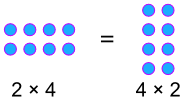
pendlande procentsatser!,

eftersom A × B = B × A är det också sant att A% av B = B% av a

exempel: 8% av 50 = 50% av 8, vilket är 4

varför ”commutative” … ?

eftersom siffrorna kan färdas fram och tillbaka som en pendlare.

associativa lagar

”associativa lagar” säger att det spelar ingen roll hur vi grupperar siffrorna (dvs. som vi beräknar först) …

…, när vi lägger till:

(a + b) + c = a + (b + c)

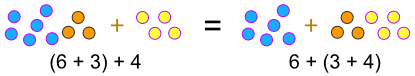
…,r>

detta: (2 + 4) + 5 = 6 + 5 = 11 har samma svar som detta: 2 + (4 + 5) = 2 + 9 = 11

detta: (3 × 4) × 5 = 12 × 5 = 60
har samma svar som detta: 3 × (4 × 5) = 3 × 20 = 60

använder sig av:

Ibland är det lättare att lägga till eller multiplicera i en annan ordning:

Vad är det? 19 + 36 + 4?,

19 + 36 + 4 = 19 + (36 + 4)
= 19 + 40 = 59

eller för att omorganisera lite:

vad är 2 × 16 × 5?

2 × 16 × 5 = (2 × 5) × 16
= 10 × 16 = 160

distributiv lag

”distributiv lag” är den bästa av alla, men behöver noggrann uppmärksamhet.,

detta är vad det låter oss göra:

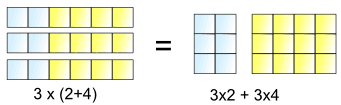
3 massor av (2+4) är densamma som 3 massor av 2 plus 3 massor av 4

så, 3× kan ”distribueras” över 2+4, till 3×2 och 3×4

och vi skriver det så här:

a × (b + c) = a × b + a × c

prova beräkningarna själv:

  • 3 × (2 + 4) = 3 × 6 = 18
  • 3×2 + 3×4 = 6 + 12 = 18

hur som helst får samma svar.,

på engelska kan vi säga:

vi får samma svar när vi:

  • multiplicera ett tal med en grupp av siffror som läggs ihop, eller
  • multiplicera var och en separat och lägg sedan till dem

använder:

Ibland är det lättare att bryta upp en svår multiplikation:

exempel: vad är 6 × 204 ?

6 × 204 = 6×200 + 6×4
= 1,200 + 24
= 1,224

eller att kombinera:

exempel: vad är 16 × 6 + 16 × 4?,

16 × 6 + 16 × 4 = 16 × (6+4)
= 16 × 10
= 160

Vi kan använda den i subtraktion också:

exempel: 26×3 – 24×3

26×3 – 24×3 = (26 – 24) × 3
= 2 × 3
= 6

Vi kan också använda den för en lång lista med tillägg:

exempel: 6×7 + 2×7 + 3×7 + 5×7 + 4×7

6×7 + 2×7 + 3×7 + 5×7 + 4×7
= (6+2+3+5+4) × 7
= 20 × 7
= 140

. . . men gå inte för långt!,

den kommutativa lagen fungerar inte för subtraktion eller division:

exempel:

  • 12 / 3= 4, men
  • 3 / 12 = ¼

den associativa lagen fungerar inte för subtraktion eller division: